题目内容
17.已知f(x)=9x-2a•3x+4.(I)令t=3x,求t在区间[-1,2]上的值域;
(2)若a=1,求函数f(x)的值域;
(3)若a>0,求f(x)在区间[1,2]上的最小值.
分析 (1)设t=3x,由 x∈[-1,2],且函数t=3x 在[-1,2]上是增函数,故有 $\frac{1}{3}$≤t≤9,由此求得t的最大值和最小值.
(2)由f(x)=t2-2t+4=(t-1)2+3,可得此二次函数的对称轴为 t=1,且 $\frac{1}{3}$≤t≤9,由此求得f(x)的最大值与最小值.
(3)讨论对称轴,结合二次函数的性质进行求解即可.
解答 解:(1)设t=3x,∵x∈[-1,2],函数t=3x 在[-1,2]上是增函数,故有 $\frac{1}{3}$≤t≤9,故t的最大值为9,t的最小值为$\frac{1}{3}$.
(2)当a=1时,由f(x)=9x-2×3x+4=t2-2t+4=(t-1)2+3,可得此二次函数的对称轴为 t=1,且 $\frac{1}{3}$≤t≤9,
故当t=1时,函数f(x)有最小值为3,
当t=9时,函数f(x)有最大值为 67.
即函数的值域为[3,67].
(3)设t=3x,∵x∈[1,2],
∴设t∈[3,9],
则y=g(t)=9x-2a•3x+4=t2-2at+4=(t-a)2+4-a2,对称轴为t=a,
若a≤3,则函数的最小值为g(3)=13-6a,
当a≥9,则函数的最小值为g(9)=85-18a,
当3≤a≤9,则函数的最小值为g(a)=4-a2.
点评 本题主要考查指数函数的综合题,求二次函数在闭区间上的最值,利用换元法结合二次函数的性质是解决本题的关键.属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
7.如图,四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{DC}$,则必有( )
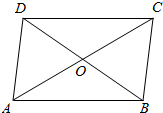

| A. | $\overrightarrow{AD}$=$\overrightarrow{CB}$ | B. | $\overrightarrow{OA}$=$\overrightarrow{OC}$ | C. | $\overrightarrow{AC}$=$\overrightarrow{DB}$ | D. | $\overrightarrow{DO}$=$\overrightarrow{OB}$ |
8.已知$sin(a+\frac{π}{6})-cosa=\frac{1}{3},则cos(2a-\frac{π}{3})$=( )
| A. | -$\frac{5}{18}$ | B. | $\frac{5}{18}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
2.不等式|3x+6|≤21的解集是( )
| A. | ∅ | B. | [-9,5] | C. | (-∞,-9)∪(5,+∞) | D. | R |
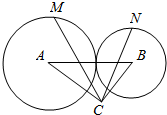 如图,圆A与圆B外切,半径分别为3,2,且△ABC是以C为直角顶点的Rt△.若AC=4.BC=3,点M,N分别在圆A,B上,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是[-6-$\sqrt{145}$,6+$\sqrt{145}$].
如图,圆A与圆B外切,半径分别为3,2,且△ABC是以C为直角顶点的Rt△.若AC=4.BC=3,点M,N分别在圆A,B上,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是[-6-$\sqrt{145}$,6+$\sqrt{145}$].