题目内容
9.函数f(x)=Acos(ωx+φ)(A>0,ω>0)在x=2015处取得最小值,则( )| A. | f(x-2015)一定是奇函数 | B. | f(x-2015)一定是偶函数 | ||
| C. | f(x+2015)一定是奇函数 | D. | f(x+2015)一定是偶函数 |
分析 由题意可得直线x=2015为函数f(x)的一条对称轴,由函数图象变换可得y值为函数f(x+2015)的一条对称轴,可得偶函数.
解答 解:∵函数f(x)=Acos(ωx+φ)在x=2015处取得最小值,
∴直线x=2015为函数f(x)的一条对称轴,
∴f(x+2015)的图象是f(x)的图象左移2015个单位得到的,
∴x=0(即y轴)为函数f(x+2015)的一条对称轴,
∴f(x+2015)一定是偶函数,
故选:D.
点评 本题考查正弦函数图象的对称性,涉及函数的奇偶性和图象变换,属基础题.

练习册系列答案
相关题目
1.已知$\overrightarrow{a}$=2,$\overrightarrow{b}$=1,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=5,则$\overrightarrow{a}$,$\overrightarrow{b}$夹角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2\sqrt{3}}{5}$ | D. | $\frac{\sqrt{2}}{2}$ |
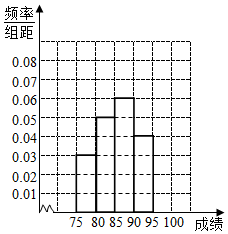 将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.
将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分. 函数f(x)=sin(ωx+φ)(ω>0,φ∈[0,2π])的部分图象如图所示,则f(2013)=-1.
函数f(x)=sin(ωx+φ)(ω>0,φ∈[0,2π])的部分图象如图所示,则f(2013)=-1.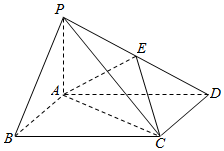 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.