题目内容
14．已知函数f（x）=2（x-m）2+8x-1的对称轴为x+1=0，则m=1；当-2＜x≤2时，最小值为-1，值域为17．分析 整理不等式可得f（x）=2x2-（4m-8）x+2m2-1，根据对称轴求出m值，利用二次函数性质求出最值．
解答 解：f（x）=2（x-m）2+8x-1
=2x2-（4m-8）x+2m2-1，
对称轴为x=$\frac{4m-8}{4}$=-1，
∴m=1；
f（x）=2x2+4x+1，
当-2＜x≤2时，
最小值为f（-1）=-1，最大值为f（2）=17．
点评 考查了二次函数的性质．属于基础题型，应熟练掌握．
练习册系列答案
相关题目
9．
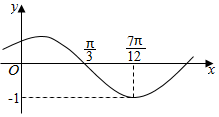已知函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，将函数f（x）的图象向左平移$\frac{π}{6}$个单位长度得到函数g（x）的图象，则函数g（x）的解析式为（ ）
已知函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，将函数f（x）的图象向左平移$\frac{π}{6}$个单位长度得到函数g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=sin（2x-$\frac{π}{3}$） | B． | g（x）=sin（2x+$\frac{π}{6}$） | C． | g（x）=-sin（2x-$\frac{π}{3}$） | D． | g（x）=sin（4x+$\frac{π}{6}$） |
2．在△ABC中，B=$\frac{π}{3}$，AB=2，D为AB中点，△BCD的面积为$\frac{3\sqrt{3}}{4}$，则AC等于（ ）
| A． | 2 | B． | $\sqrt{7}$ | C． | $\sqrt{10}$ | D． | $\sqrt{19}$ |
9．函数f（x）=Acos（ωx+φ）（A＞0，ω＞0）在x=2015处取得最小值，则（ ）
| A． | f（x-2015）一定是奇函数 | B． | f（x-2015）一定是偶函数 | ||
| C． | f（x+2015）一定是奇函数 | D． | f（x+2015）一定是偶函数 |
6．下列叙述正确的是（ ）
| A． | 数列1，3，5，7与7，5，3，1是相同的数列 | |
| B． | 数列0，1，2，3，…可以表示为{n} | |
| C． | 数列0，1，0，1，…是常数列 | |
| D． | 数列{$\frac{n}{n+1}$}是递增数列 |
如图，在四棱锥P-ABCD中，底面ABCD为菱形，其中PA=PD=AD=2，∠BAD=60°，点M在线段PC上，且PM=2MC，N为AD的中点．