Question

7．设函数f（x）=x²+ax+b（a，b∈R）．
（1）若g（x）=$\frac{f（x）}{x+1}$，当a=1，b=2时，求g（x）在[0，1]上的最小值；
（2）若h（x）=f（2^x-2^-x）+2^2x+2^-2x，b=2，求h（x）在[1，+∞）上的最小值m（a）的解析式；
（3）若存在x∈[0，1]，使得f（x）=0，且0≤b-2a≤1，求b的取值范围．

Answer 1

分析 （1）当a=1，b=2时，g（x）=$\frac{f（x）}{x+1}$=x+$\frac{2}{x+1}$，利用导数法，分析函数的单调性，进而可得函数的最值；
（2）当b=2时，f（x）=x²+ax+2，h（x）=f（2^x-2^-x）+2^2x+2^-2x=2（2^x-2^-x）²+a（2^x-2^-x）+4，令t=2^x-2^-x，结合二次函数的图象和性质，可得h（x）在[1，+∞）上的最小值m（a）的解析式；
（3）若存在x∈[0，1]，使得f（x）=0，且0≤b-2a≤1，则f（0）=b≥0，f（1）=1+a+b≤0，或f（0）=b≤0，f（1）=1+a+b≥0，又由0≤b-2a≤1，结合线性规划的知识，可得b的范围．

解答 解：（1）当a=1，b=2时，g（x）=$\frac{f（x）}{x+1}$=$\frac{{x}^{2}+x+2}{x+1}$=x+$\frac{2}{x+1}$，
则g′（x）=1-$\frac{2}{（x+1）^{2}}$=$\frac{{x}^{2}+2x-1}{{（x+1）}^{2}}$，
令g′（x）=0，则x=-1-$\sqrt{2}$，或x=-1+$\sqrt{2}$，
当x∈[0，-1+$\sqrt{2}$]时，g′（x）＜0，g（x）为减函数；
当x∈[-1+$\sqrt{2}$，1]时，g′（x）＞0，g（x）为增函数；
故当x=-1+$\sqrt{2}$时，g（x）取最小值2$\sqrt{2}$-1；
（2）当b=2时，f（x）=x²+ax+2，
h（x）=f（2^x-2^-x）+2^2x+2^-2x=2（2^x-2^-x）²+a（2^x-2^-x）+4，
令t=2^x-2^-x，x∈[1，+∞），则t∈[$\frac{3}{2}$，+∞），
y=h（x）=2t²+at+4，t∈[$\frac{3}{2}$，+∞），
由y=2t²+at+4的图象是开口朝上，且以t=-$\frac{a}{4}$为对称轴的抛物线，
故当-$\frac{a}{4}$≤$\frac{3}{2}$，即a≥-6时，m（a）=$y{|}_{t=\frac{3}{2}}$=h（1）=$\frac{1}{2}$（3a+17）；
当-$\frac{a}{4}$＞$\frac{3}{2}$，即a＜-6时，m（a）=$y{|}_{t=-\frac{a}{4}}$=4-$\frac{{a}^{2}}{8}$$\frac{{a}^{2}}{8}$；
综上所述，m（a）=$\left\{\begin{array}{l}\frac{1}{2}（3a+17），a≥-6\\ 4-\frac{{a}^{2}}{8}，a＜-6\end{array}\right.$
（3）若存在x∈[0，1]，使得f（x）=0，
则f（0）=b≥0，f（1）=1+a+b≤0，
或f（0）=b≤0，f（1）=1+a+b≥0，
又由0≤b-2a≤1，
故（a，b）对应的平面区域如下图所示：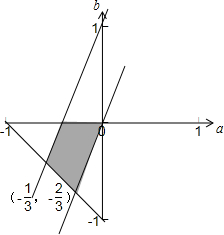

故b∈[-$\frac{2}{3}$，0]

点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．