题目内容
6．设全集U=R，A=$\left\{{x|\frac{1}{{|{x-1}|}}＜1}\right\}，B=\left\{{x|{x^2}-5x+4＞0}\right\}$，则A∩（∁UB）={x|2＜x≤4}．分析 解不等式求出集合A、B，根据补集与交集的定义写出A∩（∁UB）．
解答 解：全集U=R，A={x|$\frac{1}{|x-1|}$＜1}={x||x-1|＞1}={x|x＜0或x＞2}；
B={x|x2-5x+4＞0}={x|x＜1或x＞4}，
∴∁UB={x|1≤x≤4}，
∴A∩（∁UB）={x|2＜x≤4}．
故答案为：{x|2＜x≤4}．
点评 本题考查了解不等式与集合的基本运算问题，是基础题．
练习册系列答案
相关题目
16．在平行四边形ABCD中，∠BAD=60°，E是CD上一点，且$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{BC}$，|$\overrightarrow{AB}$|=λ|$\overrightarrow{AD}$|．若$\overrightarrow{AC}$•$\overrightarrow{EB}$=$\frac{1}{2}$$\overrightarrow{AD}$2，则λ等于（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | 3 |
17．已知a＜0，则“ax0=b”的充要条件是（ ）
| A． | ?x∈R，$\frac{1}{2}$ax2-bx≥$\frac{1}{2}$ax02-bx0 | B． | ?x∈R，$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax02-bx0 | ||
| C． | ?x∈R，$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax02-bx0 | D． | ?x∈R，$\frac{1}{2}$ax2-bx≥$\frac{1}{2}$ax02-bx0 |
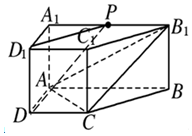直棱柱ABCD-A1B1C1D1中，底面ABCD是直角梯形，∠BAD=∠ADC=90°，AB=2AD=2CD=2．P为A1B1的中点