题目内容
14.已知数列{bn}是等比数列,其通项公式为bn=5•2n-3,公比q=2,前n项和为Sn,证明:数列{Sn+$\frac{5}{4}$}是等比数列.分析 根据等比数列的通项公式求出首项,再根据前n项和公式求出Sn,即可得到Sn+$\frac{5}{4}$=5•2n-3=bn,问题得以证明.
解答 证明:∵数列{bn}是等比数列,其通项公式为bn=5•2n-3,公比q=2,
∴b1=$\frac{5}{4}$,
∴Sn=$\frac{\frac{5}{4}(1-{2}^{n})}{1-2}$=5•2n-3-$\frac{5}{4}$,
∴Sn+$\frac{5}{4}$=5•2n-3=bn,
∴数列{Sn+$\frac{5}{4}$}是等比数列.
点评 本题考查了等比数列的通项公式和前n项和公式,属于基础题.

练习册系列答案
相关题目
9.有4种树木和5种花卉,某小区物业打算从中选出2种树木和3种花卉进行小区绿化,则不同选择方案的种数为( )
| A. | 6 | B. | 16 | C. | 60 | D. | 720 |
4.已知实数a,b,c满足a>b>c,则下列结论正确的是( )
| A. | ac>bc | B. | ac>bc | C. | ca>cb | D. | 2a>2b |
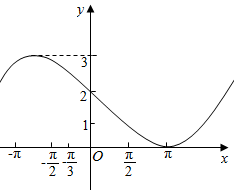 已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的一段图象(如图所示).
已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的一段图象(如图所示).