题目内容
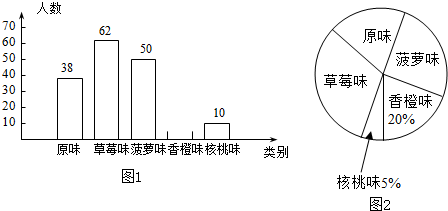
4．某次抽奖活动在三个箱子中均放有红、黄、绿、蓝、紫、橙、白、黑8种颜色的球各一个，奖励规则如下：从三个箱子中分别摸出一个球，摸出的3 个球均为红球的得一等奖，摸出的3个球中至少有一个绿球的得二等奖，摸出的3个球均为彩色球（黑、白除外）的得三等奖．问不中奖的概率是多少？（ ）| A． | 在0～25%之间 | B． | 在25～50%之间 | C． | 在50～75%之间 | D． | 在75～100%之间 |
分析 根据已知中奖励规则，先计算出各级奖项的中奖概率，得到中奖的概率，再根据对立事件概率减法公式，求出不中奖原概率，可得答案．
解答 解：∵三个箱子中均放有红、黄、绿、蓝、紫、橙、白、黑8种颜色的球各一个，
从三个箱子中分别摸出一个球，摸出的3 个球均为红球的概率为：（$\frac{1}{8}$）3=$\frac{1}{512}$，
摸出的3个球中至少有一个绿球的概率为：1-（$\frac{7}{8}$）3=$\frac{169}{512}$，
摸出的3个球均为彩色球且不含绿球的概率为：（$\frac{5}{8}$）3=$\frac{125}{512}$，
故中奖的概率为：$\frac{1}{512}$+$\frac{169}{512}$+$\frac{125}{512}$=$\frac{295}{512}$，
故不中奖的概率为：1-$\frac{295}{512}$=$\frac{217}{512}$≈42%，
故选：B
点评 本题考查的知识点是相互独立事件的概率乘法公式，对立事件的概率减法公式，难度中档．
练习册系列答案
相关题目
15．
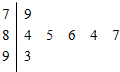在广雅中学“十佳学生”评选的演讲比赛中，如图是七位评委为某学生打出的分数的茎叶图，去掉一个最高分和一个最低分后，所剩数据的众数和中位数分别为（ ）
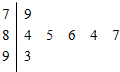在广雅中学“十佳学生”评选的演讲比赛中，如图是七位评委为某学生打出的分数的茎叶图，去掉一个最高分和一个最低分后，所剩数据的众数和中位数分别为（ ）| A． | 85，85 | B． | 84，86 | C． | 84，85 | D． | 85，86 |
正三角形ABC的边长为2，将它沿高AD翻折，使BD⊥CD，此时四面体ABCD外接球表面积为5π．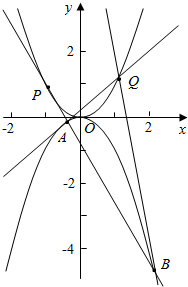
如图，过抛物线${C_1}：{x^2}=2py$上的一点Q与抛物线${C_2}：{x^2}=-2py$相切于A，B两点．若抛物线${C_1}：{x^2}=2py$的焦点F1到抛物线${C_2}：{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$