题目内容
我们把棱长要么为2cm,要么为3cm的三棱锥定义为“和谐棱锥”.在所有结构不同的“和谐棱锥”中任取一个,取到有且仅有一个面是等边三角形的“和谐棱锥”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:列举出所有的情形,由古典概型公式可得.
解答:
解:结构不同的“和谐棱锥”的六条棱的长度共有6种情况:
①六个2;②五个2和一个3;
③四个2和两个3,此时有两种情形,棱长为3的两条棱共面和异面;
④三个2和三个3,此时有3种情形;
⑤两个2和4个3,此时有2种情形;
⑥一个2和5个3;⑦六个3.
有且仅有一个面是等边三角形的情况共有4个,
④三个2和三个3中有2种情形,③四个2和两个3和⑤两个2和4个3各有1个符合,
故取到有且仅有一个面是等边三角形的“和谐棱锥”的概率是
,
故选:D.
①六个2;②五个2和一个3;
③四个2和两个3,此时有两种情形,棱长为3的两条棱共面和异面;
④三个2和三个3,此时有3种情形;
⑤两个2和4个3,此时有2种情形;
⑥一个2和5个3;⑦六个3.
有且仅有一个面是等边三角形的情况共有4个,
④三个2和三个3中有2种情形,③四个2和两个3和⑤两个2和4个3各有1个符合,
故取到有且仅有一个面是等边三角形的“和谐棱锥”的概率是
| 4 |
| 11 |
故选:D.
点评:本题考查古典概型问题,列举法是解决古典概型问题的一种重要的解题方法,属基础题.

练习册系列答案
相关题目
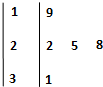 已知某篮球运动员2013年度参加了25场比赛,若从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为 ( )
已知某篮球运动员2013年度参加了25场比赛,若从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为 ( )| A、4 | ||
B、
| ||
| C、18 | ||
| D、16 |
数列{an}的通项公式是关于x的不等式x2-x≤nx(n∈N*)的解集中的整数个数,则数列{
}的前n项和Sn=( )
| 1 |
| anan+1 |
A、
| ||
| B、n(n+1) | ||
C、
| ||
D、
|
函数y=x2+4x+7的图象按向量
经过一次平移后得到y=x2的图象,则
=( )
| a |
| a |
| A、(2,3) |
| B、(-2,3) |
| C、(-2,-3) |
| D、(2,-3) |
在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽取3件,恰好有一件是次品的抽法有( )
| A、9506种 |
| B、9508种 |
| C、9604种 |
| D、9606种 |
若|
|=1,|
|=2,|
+
|=
,则
与
的夹角θ的余弦值为( )
| a |
| b |
| a |
| b |
| 7 |
| a |
| b |
A、-
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
