题目内容
已知函数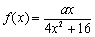 ,
,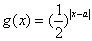 ,其中a∈R.
,其中a∈R.
(1)若0<a≤2,试判断函数h(x)=f (x)+g (x) 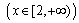 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(2)设函数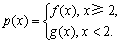 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得p (x1) = p (x2) 成立,试确定实数a的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得p (x1) = p (x2) 成立,试确定实数a的取值范围.
(1)h (x)为单调减函数.证明:由0<a≤2,x≥2,可得
 =
=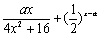 =
=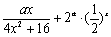 .
.
由 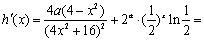
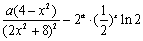 ,
,
且0<a≤2,x≥2,所以 .从而函数h(x)为单调减函数. (亦可先分别用定义法或导数法论证函数
.从而函数h(x)为单调减函数. (亦可先分别用定义法或导数法论证函数 在
在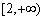 上单调递减,再得函数h(x)为单调减函数.)
上单调递减,再得函数h(x)为单调减函数.)
(2)①若a≤0,由x1≥2,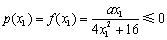 ,x2<2,
,x2<2, ,
,
所以g (x1) = g (x2)不成立.
②若a>0,由x>2时,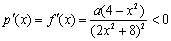 ,
,
所以p(x)在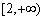 单调递减.从而
单调递减.从而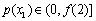 ,即
,即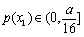 .
.
(a)若a≥2,由于x<2时,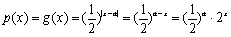 ,
,
所以p(x)在(-∞,2)上单调递增,从而 ,即
,即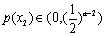 .
.
要使p (x1) = p (x2)成立,只需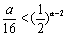 ,即
,即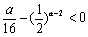 成立即可.
成立即可.
由于函数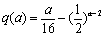 在
在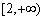 的单调递增,且q(4)=0,所以2≤a<4.
的单调递增,且q(4)=0,所以2≤a<4.
(b)若0<a<2,由于x<2时,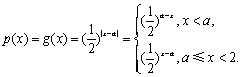
所以p(x)在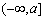 上单调递增,在
上单调递增,在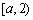 上单调递减.从而
上单调递减.从而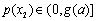 ,
,
即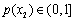 .
.
要使p (x1) = p (x2)成立,只需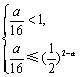 成立,即
成立,即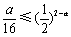 成立即可.
成立即可.
由0<a<2,得 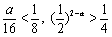 .故当0<a<2时,
.故当0<a<2时,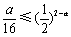 恒成立.
恒成立.
综上所述,a的取值范围为(0,4).

练习册系列答案
相关题目
 = .
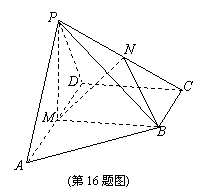
= .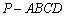 中,底面
中,底面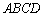 为直角梯形,
为直角梯形,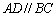 ,
,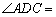 90°,
90°, ,
,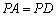 ,
,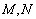 分别为
分别为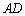 和
和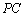 的中点.
的中点.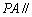 平面
平面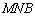 ;
;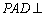 平面
平面 .
.
 恒成立,则实数a的取值范围是 .
恒成立,则实数a的取值范围是 . ≥2y+3.
≥2y+3. 上的奇函数
上的奇函数 满足
满足 ,当
,当 时,
时, ,则
,则 内是( )
内是( ) B.减函数且
B.减函数且 C.增函数且
C.增函数且 与⊙
与⊙ 相切,
相切, 为切点,过点
为切点,过点 的割线交圆于
的割线交圆于 两点,弦
两点,弦 ,
, 相交于点
相交于点 ,
, 为
为 上一点,且
上一点,且 .
. ;
; ,求
,求