题目内容
(本小题满分12分)已知 ,
, .
.
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)对一切 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)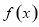 的单调递增区间
的单调递增区间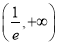 ,递减区间是
,递减区间是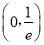 ;(2)
;(2)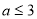 .
.
【解析】
试题分析:(1)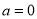 时,求导,解
时,求导,解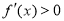 和
和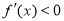 可得函数
可得函数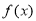 的递增区间和递减区间;
的递增区间和递减区间;
(2)对一切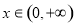 ,
,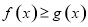 恒成立
恒成立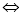
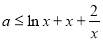 在
在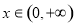 恒成立,令
恒成立,令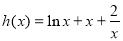 ,求
,求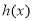 在区间
在区间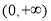 上的最小值即可.
上的最小值即可.
试题解析:(1)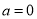 时,
时,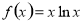 ,
, 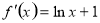 -
-
令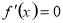 得
得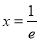 ,当
,当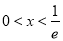 时
时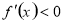 ,
,
当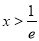 时
时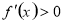
所以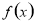 的单调递增区间
的单调递增区间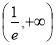 ,递减区间是
,递减区间是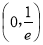
(2)对一切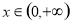 ,
,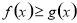 恒成立,即
恒成立,即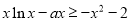 恒成立.
恒成立.
也就是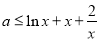 在
在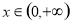 恒成立.
恒成立.
令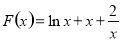 ,则
,则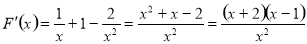
在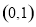 上
上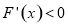 ,在
,在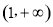 上
上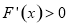 ,因此,
,因此,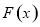 在
在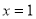 处取极小值,也是最小值,即
处取极小值,也是最小值,即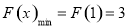 ,所以
,所以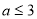
考点:导数与函数单调性、极值、不等式恒成立与分离参数.

练习册系列答案
相关题目
 中,点
中,点 是
是 的中点,过点
的中点,过点 的直线分别交直线
的直线分别交直线 ,
, 于不同的两点
于不同的两点 ,若
,若 ,
, ,则
,则 的值为 .
的值为 .
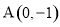 的直线
的直线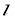 与圆
与圆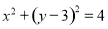 的圆心的距离记为
的圆心的距离记为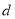 ,则
,则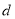 的取值范围为( )
的取值范围为( )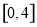 B.
B.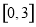 C.
C. D.
D.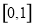
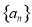 中,若
中,若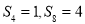 ,则
,则 的值为( )
的值为( ) ,且
,且 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 中,
中, ,则
,则 .
.
 B.
B.
 D.
D.
 中,
中, ,
, ,则
,则 .
.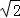 ,
, ),半径r=
),半径r=