题目内容
如图,在直三棱柱 (侧棱和底面垂直的棱柱)中,平面
(侧棱和底面垂直的棱柱)中,平面 侧面
侧面 ,
, ,
, ,且满足
,且满足 .
.

(1)求证: ;
;
(2)求点 的距离;
的距离;
(3)求二面角 的平面角的余弦值.
的平面角的余弦值.
(1)证明见解析,(2) ,(3)
,(3)
【解析】
试题分析:如何用平面 侧面
侧面 ?由面面垂直的性质定理,过
?由面面垂直的性质定理,过 作
作 ,垂足为
,垂足为 ,可知
,可知 ,有
,有 ,又
,又 ,则
,则 ,于是
,于是 即可;第二步求点
即可;第二步求点 到直线
到直线 的距离有两种方法:(1)利用体积相等,(2)利用空间向量的坐标运算,直接求法向量,用公式;第三步求二面角
的距离有两种方法:(1)利用体积相等,(2)利用空间向量的坐标运算,直接求法向量,用公式;第三步求二面角 的平面角的余弦值可运用求法向量的方法求之.
的平面角的余弦值可运用求法向量的方法求之.
试题解析:(1)证明:如右图,过 作
作 ,垂足为
,垂足为 ,因平面
,因平面 侧面
侧面 , 且平面
, 且平面 侧面
侧面
 ,可知
,可知 ,有
,有 ,又
,又 ,
, ,则
,则 ,又
,又
 平面
平面 ,所以
,所以 .因为三棱柱ABC—A1B1C1是直三棱柱,则
.因为三棱柱ABC—A1B1C1是直三棱柱,则
 底面
底面 ,所以
,所以 .又
.又

 ,从而
,从而
 侧面
侧面 ,又
,又
 侧面
侧面 ,故
,故
 .
.
(2)由(1)知,以点 为坐标原点,以
为坐标原点,以 所在的直线分别为
所在的直线分别为 轴、
轴、 轴、
轴、 轴,可建立如图所示的空间直角坐标系,
轴,可建立如图所示的空间直角坐标系, ,
,

又由线段 上分别有一点
上分别有一点 ,满足
,满足 ,所以
,所以 ,
, ,
,

 所以
所以 ,
,
所以点 的距离
的距离 .
.
(3)设平面  的法向量为
的法向量为 ,易知平面
,易知平面  的法向量可以为
的法向量可以为 .由
.由
 ,令
,令 ,则
,则 ,可得平面
,可得平面  的一个法向量可为
的一个法向量可为 ,设
,设 与
与 的夹角为
的夹角为 .则
.则 ,易知二面角
,易知二面角 的平面角为钝角,故应为角
的平面角为钝角,故应为角 的补角,所以其余弦值为
的补角,所以其余弦值为 .
.
考点:1.线线垂直、线面垂直、面面垂直的转化;2.求点到平面距离;3.二面角;

练习册系列答案
相关题目
 ,则
,则 的值是
的值是 B.
B. C.
C. D.
D.
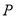 是抛物线
是抛物线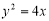 上的一个动点,
上的一个动点,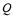 是圆
是圆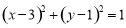 上的一个动点,
上的一个动点,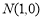 是一个定点,则
是一个定点,则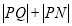 的最小值为( )
的最小值为( )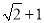
 ,则抛物线的方程是( )
,则抛物线的方程是( ) B.
B. C.
C. D.
D.
 的焦点分别为
的焦点分别为 和
和 ,点
,点 在椭圆上,如果线段
在椭圆上,如果线段 的中点在
的中点在 轴上,那么
轴上,那么 。
。 上一点
上一点 到直线
到直线 的距离与到点
的距离与到点 的距离之差的最大值为( )
的距离之差的最大值为( ) B.
B. C.
C. D.
D.
 上一点,则
上一点,则 的最大值为
的最大值为 C.
C.  D.
D. 
 的左、右焦点为
的左、右焦点为 ,
, ,其上一点
,其上一点 满足
满足 ,则点
,则点