题目内容
已知极点与原点重合,极轴与x轴正半轴重合,若直线C1的极坐标方程为:ρcos(θ-
)=
,曲线C2的参数方程为:
(θ为参数),试求曲线C2关于直线C1对称的曲线的直角坐标方程.
| π |
| 4 |
| 2 |
|
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:曲线C1可化为直角坐标方程,曲线C2是以(1,3)为圆心,1为半径的圆,求出(1,3)关于直线x+y=2的对称点,即可求出圆的方程.
解答:
解:曲线C1可化为:
ρcosθ+
ρsinθ=
,即x+y=2…(5分)
曲线C2是以(1,3)为圆心,1为半径的圆…(6分)
设(1,3)关于直线x+y=2的对称点为(x,y),则
,
∴x=-1,y=1,即(1,3)关于直线x+y=2的对称点为(-1,1),
故所求曲线为圆(x+1)2+(y-1)2=1.…(7分)
| ||
| 2 |
| ||
| 2 |
| 2 |
曲线C2是以(1,3)为圆心,1为半径的圆…(6分)
设(1,3)关于直线x+y=2的对称点为(x,y),则
|
∴x=-1,y=1,即(1,3)关于直线x+y=2的对称点为(-1,1),
故所求曲线为圆(x+1)2+(y-1)2=1.…(7分)
点评:本题考查点的极坐标和直角坐标的互化,以及轨迹方程的求解,属于中档题.

练习册系列答案
相关题目
执行如图的程序框图,若M=
,则输出的n=( )

| 7 |
| 8 |

| A、2 | B、3 | C、4 | D、5 |
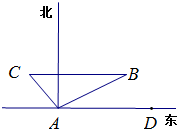 如图,海警观察站设在海岸A处,某天值班海警发现北偏东60°方向,距离A处10
如图,海警观察站设在海岸A处,某天值班海警发现北偏东60°方向,距离A处10 如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=x(x≥0)重合,点B的纵坐标为
如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=x(x≥0)重合,点B的纵坐标为