题目内容
某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
分数段(分) | |
|
|
频数 | 4 | ||
频率 | | 0.45 | 0.2 |

(Ⅰ)求表中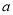 的值及分数在
的值及分数在 范围内的学生人数;
范围内的学生人数;
(Ⅱ)从得分在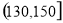 内的学生随机选2名学生的得分,求2名学生的平均分不低于140分的概率.
内的学生随机选2名学生的得分,求2名学生的平均分不低于140分的概率.
(Ⅰ)0.35;(Ⅱ)
【解析】
试题分析:(Ⅰ)由已知可得分数在 范围内的共有
范围内的共有 人,而在
人,而在 内的有4人,
内的有4人,
所以在 内的学生人数共有
内的学生人数共有 人.在
人.在 内的共有
内的共有 人,故
人,故 ;(Ⅱ)由茎叶图可知得分在
;(Ⅱ)由茎叶图可知得分在 范围内的成绩共有4个. 选取成绩的所有可能结果为
范围内的成绩共有4个. 选取成绩的所有可能结果为 ,
, ,
, ,
, ,
, ,
, ,共有6个基本事件,两个成绩之和大于
,共有6个基本事件,两个成绩之和大于 ,所以可能结果为:
,所以可能结果为:  ,
, ,
, 共3个. 所以所求事件的概率为
共3个. 所以所求事件的概率为
试题解析:(Ⅰ)由已知可得分数在 范围内的共有
范围内的共有 人,而在
人,而在 内的有4人,
内的有4人,
所以在 内的学生人数共有
内的学生人数共有 人.在
人.在 内的共有
内的共有 人,
人,
故 4分
4分
(Ⅱ)设 表示事件“从得分在
表示事件“从得分在 内的学生随机选2名学生的得分,其中2名学生的平均分不低于140分”,由茎叶图可知得分在
内的学生随机选2名学生的得分,其中2名学生的平均分不低于140分”,由茎叶图可知得分在 范围内的成绩共有4个. 6分
范围内的成绩共有4个. 6分
则选取成绩的所有可能结果为 ,
, ,
, ,
, ,
, ,
, ,
,
共有6个基本事件. 9分
事件 ,也就是两个成绩之和大于
,也就是两个成绩之和大于 ,所以可能结果为:
,所以可能结果为:  ,
, ,
, 共3个. 11分
共3个. 11分
所以所求事件的概率为 12分
12分
考点:概率与统计

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案(本小题满分12分)2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达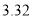 亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为
亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为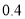 .
.
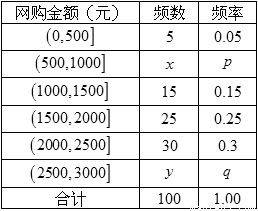

确定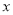 ,
,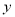 ,
,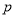 ,
,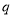 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)为进一步了解网购金额的多少是否与网龄有关,对这100名网购者调查显示:购物金额在2000元以上的网购者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的网购者中网龄不足3年的有20人.
(1)请将列联表补充完整;
网龄3年以上 | 网龄不足3年 | 合计 | |
购物金额在2000元以上 | 35 | ||
购物金额在2000元以下 | 20 | ||
合计 | 100 |
(2)并据此列联表判断,是否有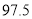 %的把握认为网购金额超过2000元与网龄在三年以上有关?
%的把握认为网购金额超过2000元与网龄在三年以上有关?
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: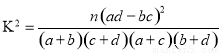 ,其中
,其中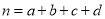 )
)



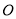 的直线
的直线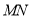 与双曲线
与双曲线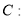
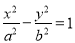 交于
交于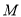 、
、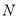 两点,
两点,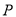 是双曲线
是双曲线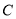 上异于
上异于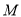 、
、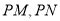 的斜率之积
的斜率之积 ,则双曲线
,则双曲线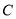 的离心率
的离心率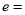
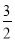 B.
B. C.
C.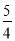 D.2
D.2 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,则下列命题中正确的是
是三个不同的平面,则下列命题中正确的是 B.若
B.若
 D.若
D.若
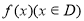 ,若
,若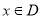 时,恒有
时,恒有 成立,则称函数
成立,则称函数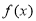 是
是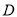 上 的“
上 的“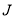 函数”.
函数”.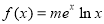 是定义域上的“
是定义域上的“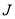 函数”时,求实数
函数”时,求实数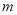 的取值范围;
的取值范围;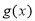 为
为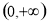 上的“
上的“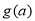 与
与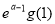 的大小(其中
的大小(其中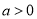 );
);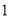 的实数
的实数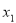 ,
,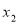 ,
,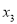 ,,
,,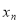 均有
均有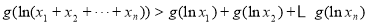 .
. 到图形
到图形 上所有点的距离的最小值为“点
上所有点的距离的最小值为“点 到图形C的距离”,那么平面内到定圆C的距离与到定点
到图形C的距离”,那么平面内到定圆C的距离与到定点 的距离相等的点的轨迹不可能是
的距离相等的点的轨迹不可能是 

 B.
B. C.
C. D.
D.
 = .
= .














