题目内容
对于函数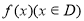 ,若
,若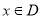 时,恒有
时,恒有 成立,则称函数
成立,则称函数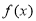 是
是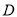 上 的“
上 的“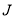 函数”.
函数”.
(Ⅰ)当函数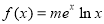 是定义域上的“
是定义域上的“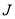 函数”时,求实数
函数”时,求实数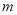 的取值范围;
的取值范围;
(Ⅱ)若函数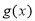 为
为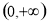 上的“
上的“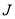 函数”.
函数”.
(ⅰ)试比较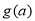 与
与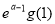 的大小(其中
的大小(其中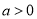 );
);
(ⅱ)求证:对于任意大于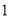 的实数
的实数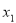 ,
,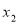 ,
,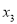 ,,
,,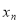 均有
均有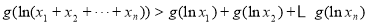 .
.
(Ⅰ)  ;(Ⅱ)见解析
;(Ⅱ)见解析
【解析】
试题分析:(Ⅰ)由 ,可得
,可得 ,因为函数
,因为函数 是
是 函数所以
函数所以 即
即
 ;(Ⅱ) (ⅰ)构造函数
;(Ⅱ) (ⅰ)构造函数 ,易得
,易得 为
为 上的增函数,当
上的增函数,当 时,
时, ,即
,即 ,得
,得 ,当
,当 时,
时, ,即
,即 ,得
,得 ,当
,当 时,
时, ,即
,即 ,得
,得 ;
;
(ⅱ)因 ,所以
,所以 所以
所以 ,
,
整理得 ,同理可得
,同理可得 ,相加即可得到证明
,相加即可得到证明
试题解析:.(Ⅰ)由 ,可得
,可得 ,因为函数
,因为函数 是
是 函数,
函数,
所以 ,即
,即 ,因为
,因为 ,
,
所以 ,即
,即 的取值范围为
的取值范围为 . 4分
. 4分
(Ⅱ)①构造函数 ,
, ,则
,则 ,
,
可得 为
为 上的增函数, 6分
上的增函数, 6分
当 时,
时, ,即
,即 ,得
,得
当 时,
时, ,即
,即 ,得
,得
当 时,
时, ,即
,即 ,得
,得 .9分
.9分
②因为 ,所以
,所以 , 10分
, 10分
由①可知 ,所以
,所以 ,
,
整理得 ,
,
同理可得 , ,
, ,  .
.
把上面 个不等式同向累加可得
个不等式同向累加可得
 14分
14分
考点:导数的综合应用、不等式证明

练习册系列答案
相关题目
某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
分数段(分) | |
|
|
频数 | 4 | ||
频率 | | 0.45 | 0.2 |

(Ⅰ)求表中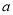 的值及分数在
的值及分数在 范围内的学生人数;
范围内的学生人数;
(Ⅱ)从得分在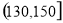 内的学生随机选2名学生的得分,求2名学生的平均分不低于140分的概率.
内的学生随机选2名学生的得分,求2名学生的平均分不低于140分的概率.
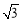 )图像上一动点,记m=
)图像上一动点,记m= , 则当m取最小值时,点P的坐标为 .
, 则当m取最小值时,点P的坐标为 . 满足约束条件
满足约束条件 ,则
,则 的最大值为_________.
的最大值为_________. 展开式中
展开式中 的系数为_________.
的系数为_________.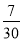 B.
B.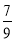 C.
C.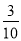 D.
D.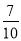



 是奇函数且
是奇函数且 ,当
,当 时,
时,  (
( ),则实数
),则实数 的值为
的值为 B.
B. C.
C. D.
D.
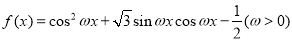 的最小正周期为
的最小正周期为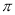 .
.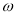 值及
值及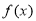 的单调递增区间;
的单调递增区间;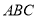 中,
中,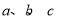 分别是三个内角
分别是三个内角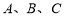 所对边,若
所对边,若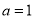 ,
,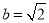 ,
,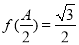 ,求
,求 的大小.
的大小. 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线 的左、右焦点.
的左、右焦点. 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;
的极坐标方程; 与圆锥曲线
与圆锥曲线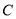 交于
交于 两点,求
两点,求 .
.