题目内容
已知下列命题中:
(1)若
•
=
•
,则
=
;
(2)向量
=(2,-3),
=(
,-
),不能作为平面内所有向量的一组基底;
(3)若向量
=(λ,2),
=(-4,-2)夹角为钝角,则λ的取值范围为λ>-1;
(4)若
∥
,
∥
,则
∥
;
(5)若三角形ABC中
•
>0,则三角形ABC为钝角三角形.
其中正确的命题序号为 .(填上所有正确的序号)
(1)若
| a |
| b |
| a |
| c |
| b |
| c |
(2)向量
| a |
| b |
| 1 |
| 2 |
| 3 |
| 4 |
(3)若向量
| a |
| b |
(4)若
| a |
| b |
| a |
| c |
| b |
| c |
(5)若三角形ABC中
| AB |
| BC |
其中正确的命题序号为
考点:平面向量数量积的运算,平行向量与共线向量
专题:平面向量及应用
分析:(1)若
•
=
•
,则
•(
-
)=0,因此不一定
=
;
(2)由
=4
,可知
,
不能作为平面内所有向量的一组基底;
(3)若向量
=(λ,2),
=(-4,-2)夹角为钝角,则
,解得即可;
(4)若
∥
,
∥
,取
=
,则
与
不一定共线;
(5)若三角形ABC中
•
>0,即
•
<0,则B为钝角.
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| b |
| c |
(2)由
| a |
| b |
| a |
| b |
(3)若向量
| a |
| b |
|
(4)若
| a |
| b |
| a |
| c |
| a |
| 0 |
| b |
| c |
(5)若三角形ABC中
| AB |
| BC |
| BA |
| BC |
解答:
解:(1)若
•
=
•
,则
•(
-
)=0,因此不一定
=
,故不正确;
(2)向量
=(2,-3),
=(
,-
),∵
=4
,∴
,
不能作为平面内所有向量的一组基底,正确;
(3)若向量
=(λ,2),
=(-4,-2)夹角为钝角,则
,解得λ的取值范围为λ>-1且λ≠4,因此不正确;
(4)若
∥
,
∥
,取
=
,则
与
不一定共线,因此不正确;
(5)若三角形ABC中
•
>0,即
•
<0,则B为钝角,则三角形ABC为钝角三角形,正确.
其中正确的命题序号为(2)(5).
故答案为:(2)(5).
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| b |
| c |
(2)向量
| a |
| b |
| 1 |
| 2 |
| 3 |
| 4 |
| a |
| b |
| a |
| b |
(3)若向量
| a |
| b |
|
(4)若
| a |
| b |
| a |
| c |
| a |
| 0 |
| b |
| c |
(5)若三角形ABC中
| AB |
| BC |
| BA |
| BC |
其中正确的命题序号为(2)(5).
故答案为:(2)(5).
点评:本题综合考查了向量的共线定理、向量垂直与数量积的关系、共面向量基本定理、向量夹角公式等基础知识与基本技能方法,考查了推理能力,属于中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
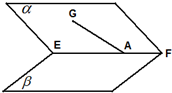 平面角为锐角的二面角α-EF-β,A∈EF,AG?α,∠GAE=45°,若AG与β所成角为30°,则二面角α-EF-β的大小是
平面角为锐角的二面角α-EF-β,A∈EF,AG?α,∠GAE=45°,若AG与β所成角为30°,则二面角α-EF-β的大小是