题目内容
数列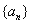 的前n项和为
的前n项和为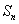 ,存在常数A,B,C,使得
,存在常数A,B,C,使得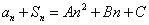 对任意正整数n都成立.
对任意正整数n都成立.
⑴若数列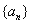 为等差数列,求证:3A-B+C=0;
为等差数列,求证:3A-B+C=0;
⑵若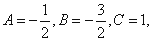 设
设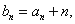 数列
数列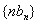 的前n项和为
的前n项和为 ,求
,求 ;
;
⑶若C=0,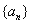 是首项为1的等差数列,设
是首项为1的等差数列,设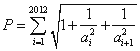 ,求不超过P的最大整数的值.
,求不超过P的最大整数的值.
⑴因为 为等差数列,设公差为
为等差数列,设公差为 ,由
,由 ,
,
得 ,
,
即 对任意正整数
对任意正整数 都成立.
都成立.
所以 所以
所以 .
.
⑵ 因为 ,所以
,所以 ,
,
当 时,
时, ,
,
所以 ,即
,即 ,
,
所以 ,而
,而 ,
,
所以数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,所以
的等比数列,所以 .
.
于是 .所以
.所以 ①,
①, ,②
,②
由① ②,
②,
得 .
.
所以 .
.
⑶ 因为 是首项为
是首项为 的等差数列,由⑴知,公差
的等差数列,由⑴知,公差 ,所以
,所以 .
.
而
 ,
,
所以 ,
,
所以,不超过 的最大整数为
的最大整数为 .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 中,⊿
中,⊿ 是等边三角形,
是等边三角形, 是以
是以 为斜边的等腰直角三角形.
为斜边的等腰直角三角形. ,求三棱锥
,求三棱锥
 中,
中, 所对的边分别为
所对的边分别为 ,E为AC边上的中点且
,E为AC边上的中点且 .
. 的大小;
的大小; ,求BE的最小值.
,求BE的最小值. ,则
,则 的值为_________。
的值为_________。 ,则该函数的值域为__________。
,则该函数的值域为__________。 函数
函数 的图象大致是( )
的图象大致是( ) ,
, ,则
,则 ( )
( ) B.
B.  C.
C.  D.
D. 