题目内容
已知a∈R,函数f(x)=4x3-2ax+a.
(1)求f(x)的单调区间;
(2)证明:当0≤x≤1时,f(x)+|2-a|>0.
解:由题意得f′(x)=12x2-2a.
当a≤0时,f′(x)≥0恒成立,此时f(x)的单调递增区间为(-∞,+∞).
当a>0时,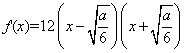 ,
,
此时函数f(x)的单调递增区间为
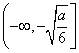 和
和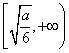 .
.
单调递减区间为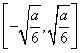 .
.
证明:由于0≤x≤1,故当a≤2时,f(x)+|a-2|=4x3-2ax+2≥4x3-4x+2.
当a>2时,f(x)+|a-2|=4x3+2a(1-x)-2≥4x3+4(1-x)-2=4x3-4x+2.
设g(x)=2x3-2x+1,0≤x≤1,
则g′(x)=6x2-2=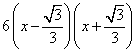 ,
,
于是在x∈(0,1)上,当x变化时,g′(x),g(x)的变化情况如下表:
| x | 0 |
|
|
| 1 |
| g′(x) | - | 0 | + | ||
| g(x) | 1 | 单调递减 | 极小值
| 单调递增 | 1 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目





 是定义在R上最小正周期为
是定义在R上最小正周期为 的函数,且在
的函数,且在 上
上 ,则
,则 的值为 .
的值为 . ,g(x)=x2-2bx+4,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),则实数b的取值范围是( )
,g(x)=x2-2bx+4,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),则实数b的取值范围是( ) B.[1,+∞] C.
B.[1,+∞] C. D.[2,+∞]
D.[2,+∞] 的部分图像可能是( )
的部分图像可能是( )

 下列结论中①
下列结论中① ②函数
②函数 的图象是中心对称图形 ③若
的图象是中心对称图形 ③若 是
是 单调递减 ④若
单调递减 ④若 . 正确的个数有( )
. 正确的个数有( )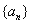 的前n项和为
的前n项和为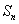 ,存在常数A,B,C,使得
,存在常数A,B,C,使得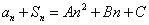 对任意正整数n都成立.
对任意正整数n都成立.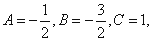 设
设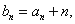 数列
数列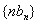 的前n项和为
的前n项和为 ,求
,求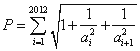 ,求不超过P的最大整数的值.
,求不超过P的最大整数的值. 平分圆
平分圆 的周长,则
的周长,则 __________。
__________。 ,
, ”是全称命题;
”是全称命题; ”的否定是“
”的否定是“ ,使
,使 ”;
”; ,则
,则 ;
;  为假命题,则
为假命题,则 、
、 均为假命题.
均为假命题.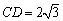 ,
,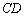 的中点为
的中点为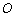 ,动点
,动点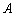 满足
满足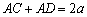 (
(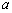 为正常数).
为正常数).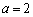 ,动点
,动点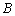 满足
满足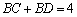 ,且
,且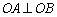 ,试求
,试求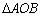 面积的最大值和最小值.
面积的最大值和最小值.