题目内容
在锐角△ABC中,若sinA=
,tanB=
,则A+B=( )
| ||
| 5 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:两角和与差的正切函数,同角三角函数间的基本关系
专题:三角函数的求值
分析:先利用同角三角函数基本关系求得tanA的值,进而利用正切的两角和公式求得tan(A+B)的值,进而求得A+B.
解答:
解:∵锐角△ABC中,sinA=
,tanB=
,
∴tanA=
∴tan(A+B)=
=
=1,
∴A+B=
,
故选B.
| ||
| 5 |
| 1 |
| 3 |
∴tanA=
| 1 |
| 2 |
∴tan(A+B)=
| tanA+tanB |
| 1-tanAtanB |
| ||||
1-
|
∴A+B=
| π |
| 4 |
故选B.
点评:本题主要考查了两角和与差的正切函数,同角三角函数基本关系的应用.考查了学生基础知识的再现和运用的能力.

练习册系列答案
相关题目
函数f(x)=2sin(x-
),x∈[-π,0]的单调递增区间是( )
| π |
| 3 |
A、[-π,-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
设
,
是夹角为
的单位向量,且
=2
+3
,
=k
-4
.若
⊥
,则实数k的值为( )
| e1 |
| e2 |
| 2π |
| 3 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
A、
| ||
B、
| ||
| C、16 | ||
| D、32 |
函数f(x)=|sinx|+
sinx(0≤x≤2π)与函数g(x)=a(a是常数)有两个不同的交点,则a的取值范围是( )
| 1 |
| 2 |
A、(0,
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
已知椭圆
+
=1(a>b>0)的左顶点为E,过原点O的直线交椭圆于A,B两点,若|AB|=|BE|=2,cos∠ABE=
,则椭圆方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
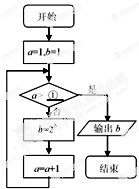 已知流程图如图(a=1,b=1下分别是a>①,b=2b,a=+1)所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填的是( )
已知流程图如图(a=1,b=1下分别是a>①,b=2b,a=+1)所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填的是( )