题目内容
13.已知f(x)是R上的减函数,a∈R,记m=f(a2),n=f(a-1),则m、n的大小关系为( )| A. | m>n | B. | m≥n | C. | m<n | D. | m≤n |
分析 通过作差比较a2和a-1的大小关系,根据f(x)是R上的减函数便可得出f(a2)与f(a-1),即m,n的大小关系.
解答 解:${a}^{2}-(a-1)={a}^{2}-a+1=(a-\frac{1}{2})^{2}+\frac{3}{4}>0$;
∴a2>a-1;
∵f(x)是R上的减函数;
∴f(a2)<f(a-1);
即m<n.
故选C.
点评 考查作差的方法比较两个式子的大小,配方法的运用,以及减函数的定义,根据减函数定义比较函数值大小的方法.

练习册系列答案
相关题目
18.已知正实数x,y满足2x+y=2,则x+$\sqrt{{x}^{2}+{y}^{2}}$的最小值为( )
| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | 2 | D. | $\frac{2+2\sqrt{2}}{3}$ |
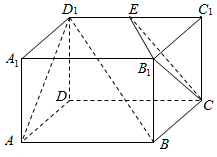 已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.