题目内容
18.已知正实数x,y满足2x+y=2,则x+$\sqrt{{x}^{2}+{y}^{2}}$的最小值为( )| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | 2 | D. | $\frac{2+2\sqrt{2}}{3}$ |
分析 由题意可得P(x,y)表示线段AB上的点,x+$\sqrt{{x}^{2}+{y}^{2}}$表示P到y轴距离d与到O的距离PO之和,由对称性解出O(0,0)关于直线2x+y=2的对称点为O′的坐标,数形结合可得.
解答  解:∵正实数x,y满足2x+y=2,∴P(x,y)表示线段AB上的点,
解:∵正实数x,y满足2x+y=2,∴P(x,y)表示线段AB上的点,
设O(0,0)关于直线2x+y=2的对称点为O′(a,b),
则由对称性可得$\left\{\begin{array}{l}{\frac{b-0}{a-0}•(-2)=-1}\\{2•\frac{a+0}{2}+\frac{b+0}{2}=2}\end{array}\right.$,解得O′($\frac{8}{5}$,$\frac{4}{5}$),
故x+$\sqrt{{x}^{2}+{y}^{2}}$表示P到y轴距离d与到O的距离PO之和.
由对称性可得PO′=PO,故原式=PO′+d,
结合图象可知当PO′与y轴垂直时上式取最小值$\frac{8}{5}$,
故选:A.
点评 本题考查式子的最值,由式子的几何意义转化为数形结合是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.设A、B、C是圆O:x2+y2=1上不同的三个点,|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\sqrt{2}$$\overrightarrow{OC}$|,若存在实数λ、μ满足$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,则点P(λ,μ)与圆O的位置关系是( )
| A. | 点P在圆内 | B. | 点P在圆上 | C. | 点P在圆外 | D. | 不确定 |
13.已知f(x)是R上的减函数,a∈R,记m=f(a2),n=f(a-1),则m、n的大小关系为( )
| A. | m>n | B. | m≥n | C. | m<n | D. | m≤n |
11.已知l、m、n是空间不同的三条直线,则下列结论中正确的( )
| A. | 若m⊥l,n⊥l,则m⊥n | B. | 若m⊥l,n⊥l,则m∥n | C. | 若m⊥l,n∥l,则m⊥n | D. | 若m⊥l,n∥l,则m∥n |
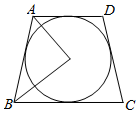 一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)
一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)