题目内容
【题目】已知![]() 是曲线
是曲线![]() 上的点,
上的点,![]() 是数列
是数列![]() 前
前![]() 项和,且满足
项和,且满足![]()
(1)若![]() 时,求
时,求![]() 的值;
的值;
(2)证明:数列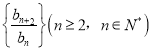 是常数列;
是常数列;
(3)确定![]() 的取值集合M,使
的取值集合M,使![]() 时,数列
时,数列![]() 是单调递增数列.
是单调递增数列.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)见详解;(3)
;(2)见详解;(3) ![]()
【解析】
(1)取![]() ,再利用
,再利用![]() 即可求得.
即可求得.
(2)根据![]() 可以得出
可以得出![]() ,再根据题意得
,再根据题意得![]() ,即可得
,即可得![]() ,即可证明.
,即可证明.
(3)根据已知条件可以推出数列![]() 和
和![]() 分别是以
分别是以![]() ,
,![]() 为首项
为首项![]() 为公差的等差数列再由数列是单调增数列能够推出
为公差的等差数列再由数列是单调增数列能够推出![]() 的取值集合.
的取值集合.
(1)![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)![]() ①,
①,
则![]() ②,
②,
由②-①得![]() ③,
③,
于是![]() ④,
④,
由④-③得![]() ⑤,
⑤,
因为![]() 是曲线
是曲线![]() 上的点,
上的点,
所以![]() ,所以
,所以![]() ,是常数,
,是常数,
即数列 是常数数列.
是常数数列.
(3)由①有![]() ,所以
,所以![]() ,由③有
,由③有![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,而⑤表明:数列
,而⑤表明:数列![]() 和
和![]() 分别是 以
分别是 以![]() ,
,![]() 为首项,
为首项,
6为公差的等差数列,所以![]() ,
,![]() ,
,
![]() ,
,
数列![]() 是单调递增数列.
是单调递增数列.![]() 且
且![]() 对任意的
对任意的![]() 成立.
成立.![]() 且
且![]() , 即所求
, 即所求![]() 的取值集合是
的取值集合是
![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目