题目内容
曲线2x2=1-y2的离心率为e1,曲线8y2=x2-32,的离心率为e2,记m=e2•e1,则( )
| A、m=1 | ||
B、m=
| ||
C、m=
| ||
D、m=
|
考点:椭圆的简单性质
专题:
分析:将曲线方程整理为标准形式,判断出两个曲线一个是椭圆,一个是双曲线,分别根据性质求出离心率即可求出m的值.
解答:
解:曲线2x2=1-y2可整理为2x2+y2=1,此是一个椭圆的方程,则a=1,b=
,可得c=
=
,故e1=
=
=
曲线8y2=x2-32可整理为x2-8y2=32,整理得
-
=1,此是一个双曲线的方程,可得a=4
,c=
=6,故e2=
=
=
∴m=e2•e1=
故选D.
| ||
| 2 |
1-
|
| ||
| 2 |
| c |
| a |
| ||||
| 1 |
| ||
| 2 |
曲线8y2=x2-32可整理为x2-8y2=32,整理得
| x2 |
| 32 |
| y2 |
| 4 |
| 2 |
| 32+4 |
| c |
| a |
| 6 | ||
4
|
3
| ||
| 4 |
∴m=e2•e1=
| 3 |
| 4 |
故选D.
点评:本题考查双曲线与椭圆的性质,基础知识考查题,较易,解答的关键是将方程整理为标准形式

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
某同学设计的算法流程图用以计算和式12+22+32+…+20152的值,则在判断框中应填写( )
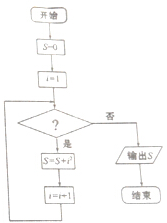

| A、i≤2015 |
| B、i≤2016 |
| C、≥2015 |
| D、i≥2016 |
已知函数y=f(x)为R上可导函数,且对?x∈R都有f(2x)=x3f′(1)-10x成立,则函数y=f(x),x∈[-1,1]的值域为( )
| A、R | B、[-6,6] |
| C、[0,6] | D、(-∞,0) |