题目内容
8.已知F1•F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点,其中F2与抛物线y2=12x的焦点重合,M是两曲线的一个交点,且有cos∠MF1F2•cos∠MF2F1=$\frac{7}{23}$,求椭圆方程.分析 先设出M的坐标,代入椭圆和抛物线方程消去y,求得M点横坐标,根据x=-3是y2=12x的准线,即抛物线的准线过椭圆的另一个焦点F1.设点P到抛物线y2=12x的准线的距离为MN,则可知|MF2|=|MN|,根据抛物线定义可知|MN|=x1+3,进而求得|MF2|和|MF1|,过点M作MM1⊥x轴,垂足为M1,分别在Rt△MM1F1中而后Rt△MM1F2中求得cos∠MF1F2,cos∠MF2F1,最后答案可得.
解答 解:抛物线y2=12x的焦点为(3,0),
即有c=3,a2-b2=9,
设M(x1,y1),
由$\left\{\begin{array}{l}{{b}^{2}{x}^{2}+{a}^{2}{y}^{2}={a}^{2}{b}^{2}}\\{{y}^{2}=12x}\end{array}\right.$得b2x2+12a2x-a2b2=0,
即为(a2-9)x2+12a2x-a2(a2-9)=0,
∴x1=$\frac{a(a-3)}{a+3}$(负的舍去),
∵x=-3是y2=12x的准线,
设点M到抛物线y2=12x的准线的距离为MN,则|MF2|=|MN|.
又|MN|=x1+3=$\frac{{a}^{2}+9}{a+3}$,
∴|MF2|=$\frac{{a}^{2}+9}{a+3}$,|MF1|=2a-$\frac{{a}^{2}+9}{a+3}$=$\frac{{a}^{2}+6a-9}{a+3}$
过点M作MM1⊥x轴,垂足为M1,
在Rt△MM1F1中,cos∠MF1F2=$\frac{a(a-3)+3(a+3)}{{a}^{2}+6a-9}$=$\frac{{a}^{2}+9}{{a}^{2}+6a-9}$,
在Rt△MM1F2中,cos∠MF2F1=$\frac{6a+9-{a}^{2}}{{a}^{2}+9}$,
由cos∠MF1F2•cos∠MF2F1=$\frac{6a+9-{a}^{2}}{{a}^{2}+6a-9}$=$\frac{7}{23}$,
解得a=5(负的舍去),
可得b=$\sqrt{{a}^{2}-{c}^{2}}$=4,
即有椭圆方程为$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1.
点评 本题主要考查了椭圆和抛物线的方程和性质,考查了椭圆和抛物线的定义的运用,考查运算能力,属于中档题.

| A. | 图象关于(π,0)中心对称 | B. | 图象关于直线x=$\frac{π}{2}$对称 | ||
| C. | g(x)是周期为π的奇函数 | D. | 在区间[-$\frac{π}{6}$,0]上单调递增 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
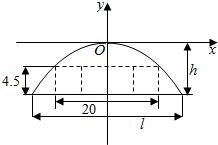 某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy.
某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy.