题目内容
18.有两块直角三角板:一块三角板的两条直角边的长分别为1,$\sqrt{3}$;另一块三角板的两条直角边的长均为$\sqrt{3}$,已知这两块三角板有两对顶点重合,且构成90°的二面角,则不重合的两个顶点间的距离等于2或$\sqrt{7}$.分析 分两种情况:①直角△ABC中,AB=1,BC=$\sqrt{3}$,∠ABC=90°,直角△CBD中,BC=BD=$\sqrt{3}$,∠CBD=90°,由此求出不重合的两个顶点间的距离;②直角△ABC中,AB=1,BC=$\sqrt{3}$,∠ABC=90°,直角△CBD中,BC=CD=$\sqrt{3}$,∠BCD=90°,由此求出不重合的两个顶点间的距离.由此能求出结果.
解答 解:∵有两块直角三角板:一块三角板的两条直角边的长分别为1,$\sqrt{3}$,
另一块三角板的两条直角边的长均为$\sqrt{3}$,
这两块三角板有两对顶点重合,且构成90°的二面角,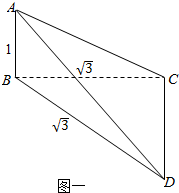
∴如图一:直角△ABC中,AB=1,BC=$\sqrt{3}$,∠ABC=90°,
直角△CBD中,BC=BD=$\sqrt{3}$,∠CBD=90°,
且平面ABC⊥平面BCD,
∴AB⊥平面BDC,∴AB⊥BD,
∴不重合的两个顶点间的距离AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=$\sqrt{1+3}$=2;
如图二:直角△ABC中,AB=1,BC=$\sqrt{3}$,∠ABC=90°,
直角△CBD中,BC=CD=$\sqrt{3}$,∠BCD=90°,
且平面ABC⊥平面BCD,
∴$BD=\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{6}$,AB⊥平面BDC,∴AB⊥BD,
∴不重合的两个顶点间的距离AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=$\sqrt{1+6}$=$\sqrt{7}$.
综上,不重合的两个顶点间的距离等于2或$\sqrt{7}$.
故答案为:2或$\sqrt{7}$.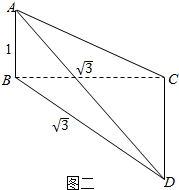
点评 本题考查两顶点间距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案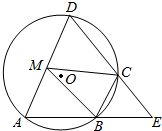 如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE. 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PO=$\sqrt{6}$.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PO=$\sqrt{6}$.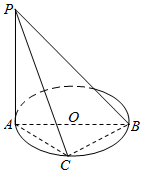 如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC
如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC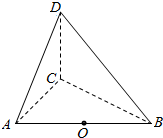 如图所示,三棱锥D-ABC中,AC,BC,CD两两垂直,AC=CD=1,$BC=\sqrt{3}$,点O为AB中点.
如图所示,三棱锥D-ABC中,AC,BC,CD两两垂直,AC=CD=1,$BC=\sqrt{3}$,点O为AB中点.