题目内容
19.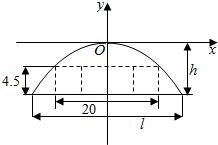 某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy.
某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy.(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)为了使施工的土方工程量最小,需隧道口截面面积最小.现隧道口的最大拱高h不小于6米,则应如何设计拱高h和拱宽l,使得隧道口截面面积最小?(隧道口截面面积公式为S=$\frac{2}{3}$lh)
分析 (1)设抛物线的方程为:y=-ax2(a>0),利用待定系数法求出$a=\frac{3}{200}$,由此能求出隧道设计的拱宽.
(2)抛物线最大拱高为h米,h≥6,利用待定系数法求出$a=\frac{{h-\frac{9}{2}}}{100}$,从而20<l≤40,S=$\frac{3{l}^{3}}{{l}^{2}-400}$,由此利用导数性质能求出当拱高为$\frac{27}{4}$米,拱宽为$20\sqrt{3}$米时,使得隧道口截面面积最小.
解答 解:(1)设抛物线的方程为:y=-ax2(a>0),则抛物线过点$(10,-\frac{3}{2})$,
代入抛物线方程解得:$a=\frac{3}{200}$,…(3分)
令y=-6,解得:x=±20,则隧道设计的拱宽l是40米.…(5分)
(2)抛物线最大拱高为h米,h≥6,抛物线过点(10,-(h-$\frac{9}{2}$)),
代入抛物线方程得:$a=\frac{{h-\frac{9}{2}}}{100}$
令y=-h,则$-\frac{{h-\frac{9}{2}}}{100}{x^2}=-h$,解得:${x}^{2}=\frac{100h}{h-\frac{9}{2}}$,
则${(\frac{l}{2})^2}=\frac{100h}{{h-\frac{9}{2}}}$,$h=\frac{\frac{9}{2}{l}^{2}}{{l}^{2}-400}$,…(9分)
∵h≥6,∴$\frac{\frac{9}{2}{l}^{2}}{{l}^{2}-400}$≥6,即20<l≤40,
∴$S=\frac{2}{3}lh=\frac{2}{3}l•\frac{{\frac{9}{2}{l^2}}}{{{l^2}-400}}=\frac{{3{l^3}}}{{{l^2}-400}}\;\;\;\;\;(20<l≤40)$,…(12分)
∴$S'=\frac{{9{l^2}({l^2}-400)-3{l^3}•2l}}{{{{({l^2}-400)}^2}}}=\frac{{3{l^2}({l^2}-1200)\;}}{{{{({l^2}-400)}^2}}}\;=\frac{{3{l^2}(l+20\sqrt{3})(l-20\sqrt{3})\;}}{{{{({l^2}-400)}^2}}}$,
当$20<l<20\sqrt{3}$时,S'<0;当$20\sqrt{3}<l≤40$时,S'>0,
即S在$(20,20\sqrt{3})$上单调减,在(20$\sqrt{3}$,40]上单调增,
∴S在$l=20\sqrt{3}$时取得最小值,此时$l=20\sqrt{3}$,$h=\frac{27}{4}$
答:当拱高为$\frac{27}{4}$米,拱宽为$20\sqrt{3}$米时,使得隧道口截面面积最小. …(15分)
点评 本题考查函数在生产生活中的具体应用,是中档题,解题时要认真审题,注意二次函数性质的合理运用,解题时要合理运用导数性质.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案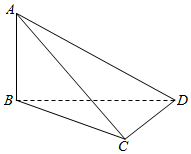 如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )| A. | 60°或90° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
| A. | ?x∉R,log2x=2015 | B. | ?x∈R,log2x≠2015 | ||
| C. | ?x0∈R,log2x0=2015 | D. | ?x0∈R,log2x0≠2015 |
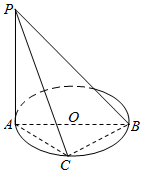 如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC
如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC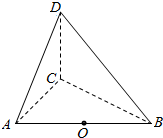 如图所示,三棱锥D-ABC中,AC,BC,CD两两垂直,AC=CD=1,$BC=\sqrt{3}$,点O为AB中点.
如图所示,三棱锥D-ABC中,AC,BC,CD两两垂直,AC=CD=1,$BC=\sqrt{3}$,点O为AB中点.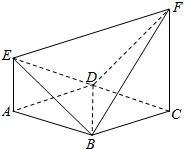 如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC∥EA,设EA=1
如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC∥EA,设EA=1