题目内容
在底面半径为2
,母线长为2
的圆锥中内接一个正四棱柱.若正四棱柱恰为正方体.
(1)求正方体的表面积和体积;
(2)求四棱柱的侧面积最大时,该四棱柱的底面边长为多少?
| 2 |
| 3 |
(1)求正方体的表面积和体积;
(2)求四棱柱的侧面积最大时,该四棱柱的底面边长为多少?
考点:棱柱、棱锥、棱台的体积,棱柱、棱锥、棱台的侧面积和表面积
专题:计算题,空间位置关系与距离
分析:(1)设正方体的边长为x,作出圆锥的轴截面;通过三角形相似解答;(2)类似于(1)分析解答.
解答:
解:∵圆锥的底面半径为2
,母线长为2
,
∴圆锥的高为
=2;
(1)设正方体的边长为x,作出圆锥的轴截面;
则由三角形相似可得,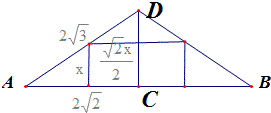
=
,
解得,x=
.
则S=6•x2=
,
V=x3=
.
(2)设四棱柱的底面边长为x,侧棱长为y,则有
=
,
则y=2-
,
S侧=4x×y=4x(2-
)=-2x2+8x=-2(x-2)2+8
则当x=2时,S侧有最大值.
即四棱柱的侧面积最大时,该四棱柱的底面边长为2.
| 2 |
| 3 |
∴圆锥的高为
| 12-8 |
(1)设正方体的边长为x,作出圆锥的轴截面;
则由三角形相似可得,

| ||||
2
|
| 2-x |
| 2 |
解得,x=
| 4 |
| 3 |
则S=6•x2=
| 32 |
| 3 |
V=x3=
| 64 |
| 27 |
(2)设四棱柱的底面边长为x,侧棱长为y,则有
| ||||
2
|
| 2-y |
| 2 |
则y=2-
| x |
| 2 |
S侧=4x×y=4x(2-
| x |
| 2 |
则当x=2时,S侧有最大值.
即四棱柱的侧面积最大时,该四棱柱的底面边长为2.
点评:本题考查了利用几何体的轴截面分析量的等量关系,注意不同量的转化.

练习册系列答案
相关题目
 如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=
如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=