题目内容
已知向量
,
,
满足
+
+
=0,且
与
的夹角为60°,|
|=
|
|,则
与
的夹角为 .
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| 3 |
| a |
| a |
| b |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:设△ABC中,
=
,
=
,
=
,令|
|=1,则|
|=
,如图:则∠ABC=120°,θ为所求.再由正弦定理可得
=
,求得sin(θ-120°)=
,可得θ的值.
| BC |
| a |
| CA |
| b |
| AB |
| c |
| BC |
| CA |
| 3 |
| AC |
| sin∠ABC |
| BC |
| sin∠BAC |
| 1 |
| 2 |
解答:
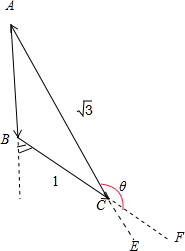 解:∵向量
解:∵向量
,
,
满足
+
+
=0,且
与
的夹角为60°,
设△ABC中,
=
,
=
,
=
,令|
|=1,则|
|=
,
如图所示:
可得∠ABC=120°,θ为所求.
△ABC中,由正弦定理可得
=
,即
=
,
求得sin(θ-120°)=
,∴θ=150°,
故答案为:150°.
 解:∵向量
解:∵向量| a |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
设△ABC中,
| BC |
| a |
| CA |
| b |
| AB |
| c |
| BC |
| CA |
| 3 |
如图所示:
可得∠ABC=120°,θ为所求.
△ABC中,由正弦定理可得
| AC |
| sin∠ABC |
| BC |
| sin∠BAC |
| ||
| sin120° |
| 1 |
| sin[180°-120°-(180°-θ)] |
求得sin(θ-120°)=
| 1 |
| 2 |
故答案为:150°.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,正弦定理的应用,体现了数形结合的数学思想,属于基础题.

练习册系列答案
相关题目