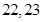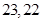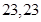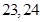题目内容
若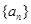 是等差数列,首项
是等差数列,首项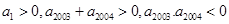 ,则使前n项和
,则使前n项和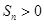 成立的最大自然数n是:( )
成立的最大自然数n是:( )
| A.4005 | B.4006 | C.4007 | D.4008 |
B
解析试题分析:根据题意可知:此等差数列的1到2003项每一项都大于0,从第2004项开始每一项都小于0,然后利用等差数列的前n项和公式表示出前4006项的和与前4007项的和,分别利用等差数列的性质变形后,根据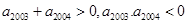 ,判断出前4005项的和为正与前4008项的和为负,即可求出满足题意的最大自然数n的值.
,判断出前4005项的和为正与前4008项的和为负,即可求出满足题意的最大自然数n的值.
由题意知:等差数列中,从第1项到第2003项是正数,且从第2004项开始为负数,结合通项公式和前n项和的关系可知,则前
故可知n的最大值为4006,选B
考点:等差数列的性质
点评:此题考查了等差数列的性质及等差数列的通项公式.本小题结论可以推广成一般结论:等差数列中,a1>0,ak+ak+1>0,且akak+1<0,则使前n项和Sn>0的最大自然数n是2k.

练习册系列答案
相关题目
已知数列 ,
, ,
,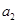 ,
, 成等差数列,
成等差数列,  ,
, ,
, ,
, ,
, 成等比数列,则
成等比数列,则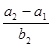 的值为( )
的值为( )
A. | B. | C. 或 或 | D. |
等差数列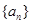 :1,4,7,……中,当
:1,4,7,……中,当 时,序号
时,序号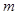 等于
等于
| A.99 | B.100 | C.96 | D.101 |
若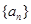 是等差数列,首项公差
是等差数列,首项公差 ,
,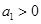 ,且
,且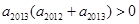 ,则使数列
,则使数列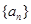 的前n项和
的前n项和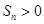 成立的最大自然数n是 ( )
成立的最大自然数n是 ( )
| A.4027 | B.4026 | C.4025 | D.4024 |
已知两个正数a,b的等差中项为4,则a,b的等比中项的最大值为( )
| A.2 | B.4 | C.8 | D.16 |
若数列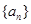 是等差数列,且
是等差数列,且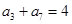 ,则数列
,则数列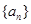 的前
的前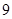 项和
项和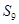 等于
等于
A.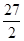 | B.18 | C.27 | D.36 |
等差数列{an}的通项公式为an=2n+1,其前n项和为Sn,则{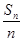 }前10项和为
}前10项和为
| A.120 | B.100 | C.75 | D.70 |
在数列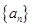 中,
中, ,
,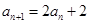 ,则
,则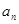 等于( )
等于( )
A.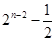 | B.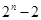 | C.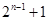 | D.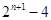 |
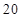 的样本数据,它们组成一个公差不为
的样本数据,它们组成一个公差不为 的等差数列
的等差数列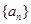 ,若
,若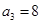 且前
且前 项和
项和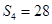 ,则此样本的平均数和中位数分别是
,则此样本的平均数和中位数分别是