题目内容
在数列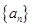 中,
中, ,
,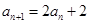 ,则
,则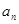 等于( )
等于( )
A.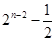 | B.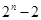 | C.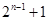 | D.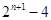 |
B
解析试题分析:因为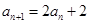 ,所以
,所以 ,
, 是等比数列
是等比数列
首项 +2=4,公比q=2
+2=4,公比q=2
∴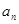 等于
等于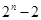 ,故选B。
,故选B。
考点:本题主要考查演绎推理的意义,等比数列通项公式。
点评:从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理。简言之,演绎推理是由一般到特殊的推理。演绎推理也称为逻辑推理。

练习册系列答案
相关题目
若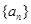 是等差数列,首项
是等差数列,首项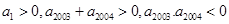 ,则使前n项和
,则使前n项和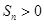 成立的最大自然数n是:( )
成立的最大自然数n是:( )
| A.4005 | B.4006 | C.4007 | D.4008 |
等差数列 的前
的前 项和为
项和为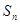 ,已知
,已知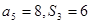 ,则
,则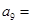 ( )
( )
A. | B. | C.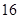 | D. |
在等差数列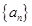 中a3+a4+a5=12,
中a3+a4+a5=12,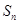 为数列
为数列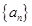 的前
的前 项和,则S7=( )
项和,则S7=( )
| A.14 | B.21 | C.28 | D.35 |
已知等差数列 中,
中,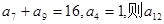 的值是( )
的值是( )
| A.15 | B.30 | C.31 | D.64 |
设 是等差数列
是等差数列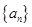 的前
的前 项和,已知
项和,已知 ,
,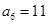 ,则
,则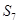 等于
等于
| A.13 | B.35 | C.49 | D.63 |
已知等差数列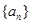 ,
, 则它的公差是( )
则它的公差是( )
| A.1 | B.2 | C.3 | D.4 |
设 是等差数列,若
是等差数列,若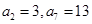 ,则数列
,则数列 前8项的和为( )
前8项的和为( )
| A.128 | B.80 | C.64 | D.56 |
设数列{2n-1}按第n组有n个数(n是正整数)的规则分组如下:(1),(2,4),(8,16,32),…,则第101组中的第一个数为( )
| A.24 951 |
| B.24 950 |
| C.25 051 |
| D.25 050 |