题目内容
已知函数f(x)=ex(x-a),a∈R.
(Ⅰ)当a=0时,求函数y=f(x)的极值;
(Ⅱ)若函数y=
在[1,+∞)单调递增,求实数a的取值范围;
(Ⅲ)试问是否存在实数x0,使得函数f(x)图象上任意不同两点连线的斜率都不等于f(x0)?若存在求出x0的值,若不存在,请说明理由.
(Ⅰ)当a=0时,求函数y=f(x)的极值;
(Ⅱ)若函数y=
| f(x) |
| x |
(Ⅲ)试问是否存在实数x0,使得函数f(x)图象上任意不同两点连线的斜率都不等于f(x0)?若存在求出x0的值,若不存在,请说明理由.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出f(x)的导数f′(x),由f′(x)正负性求出函数f(x)的单调区间,求出f(x)的极值;
(Ⅱ)由函数y=
在[1,+∞)单调递增,得y′≥0在[1,+∞)上恒成立,求出a的取值范围;
(Ⅲ)构造函数,利用函数的单调性求参数的取值范围.
(Ⅱ)由函数y=
| f(x) |
| x |
(Ⅲ)构造函数,利用函数的单调性求参数的取值范围.
解答:
解:(Ⅰ)当a=0时,f(x)=xex,f′(x)=(x+1)ex,
令f′(x)=0,得x=-1
当x>-1时,f′(x)=(x+1)ex>0;当x<-1时,f′(x)=(x+1)ex<0,
∴函数y=f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,
∴函数y=f(x)在x=-1时取得极小值-e-1,但函数没有极大值;
(Ⅱ)y′=
=
=
,
由题意得x2-ax+a≥0对x∈[1,+∞)恒成立,
即a(x-1)≤x2对x∈[1,+∞)恒成立,当x=1时不等式对a∈R恒成立,
当x≠1时,不等式化为a≤
=
=(x-1)+
+2,
由于x∈(1,+∞),所以(x-1)+
+2≥2+2=4(当且仅当x=2时时对等号),
所以a(x-1)≤x2对x∈(1,+∞)恒成立的条件是a≤4,
综上得所求实数a的范围为a≤4;
(Ⅲ)假设存在x=x0,使得对任意不同的x1,x2都有
≠f′(x0),即
f(x2)-f(x0)•x2≠f(x1)-f(x0)•x1
令g(x)=f(x)-f′(x0)•x
∵函数g(x)=f(x)-f′(x0)•x的图象连续,且对任意不同的x1,x2有g(x2)≠g(x1),
∴g′(x)=f′(x)-g′(x0)≤0(或≥0)对x∈R恒成立,
即存在x0,使得f′(x0)≥f′(x)(或f′(x0)≤f′(x))对x∈R恒成立,
令h(x)=f′(x)=(x+1-a)•ex,
令h′(x)=0得x=a-2,函数y=h(x)在(-∞,a-2)单调递减,在(a-2,+∞)单调递增,
∴函数y=h(x)在x=a-2取得最小值,
故存在x0=a-2,使得f(x)的图象上任意不同两点连线的斜率都不等于f′(x0).
令f′(x)=0,得x=-1
当x>-1时,f′(x)=(x+1)ex>0;当x<-1时,f′(x)=(x+1)ex<0,
∴函数y=f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,
∴函数y=f(x)在x=-1时取得极小值-e-1,但函数没有极大值;
(Ⅱ)y′=
| xf′(x)-f(x) |
| x2 |
| xex(x-a+1)-ex(x-a) |
| x2 |
| ex(x2-ax+a) |
| x2 |
由题意得x2-ax+a≥0对x∈[1,+∞)恒成立,
即a(x-1)≤x2对x∈[1,+∞)恒成立,当x=1时不等式对a∈R恒成立,
当x≠1时,不等式化为a≤
| x2 |
| x-1 |
| (x-1)2+2(x-1)+1 |
| x-1 |
| 1 |
| x-1 |
由于x∈(1,+∞),所以(x-1)+
| 1 |
| x-1 |
所以a(x-1)≤x2对x∈(1,+∞)恒成立的条件是a≤4,
综上得所求实数a的范围为a≤4;
(Ⅲ)假设存在x=x0,使得对任意不同的x1,x2都有
| f(x2)-f(x1) |
| x2-x1 |
f(x2)-f(x0)•x2≠f(x1)-f(x0)•x1
令g(x)=f(x)-f′(x0)•x
∵函数g(x)=f(x)-f′(x0)•x的图象连续,且对任意不同的x1,x2有g(x2)≠g(x1),
∴g′(x)=f′(x)-g′(x0)≤0(或≥0)对x∈R恒成立,
即存在x0,使得f′(x0)≥f′(x)(或f′(x0)≤f′(x))对x∈R恒成立,
令h(x)=f′(x)=(x+1-a)•ex,
令h′(x)=0得x=a-2,函数y=h(x)在(-∞,a-2)单调递减,在(a-2,+∞)单调递增,
∴函数y=h(x)在x=a-2取得最小值,
故存在x0=a-2,使得f(x)的图象上任意不同两点连线的斜率都不等于f′(x0).
点评:本题主要考查函数、导数等基础知识,考查推理能力、运算求解能力,考查化归与转化思想、分类与整合思想、函数与方程思想、数形结合思想等.

练习册系列答案
相关题目
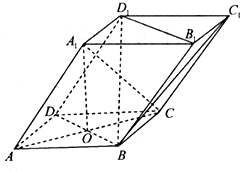 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC,BD交于点O,A1O⊥平面ABCD,A1A=BD=2,AC=2
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC,BD交于点O,A1O⊥平面ABCD,A1A=BD=2,AC=2 已知正方体ABCD-A1B1C1D1,求证:
已知正方体ABCD-A1B1C1D1,求证: 如图,在四棱柱ABCD=A1B1C1D1中,侧棱AA1⊥底面ABCD,DC=DD1=2AD=2AB=2,AD⊥DC,AB∥DC.
如图,在四棱柱ABCD=A1B1C1D1中,侧棱AA1⊥底面ABCD,DC=DD1=2AD=2AB=2,AD⊥DC,AB∥DC.