题目内容
已知A={x|a≤x≤2a+3}，B={x|x2+5x﹣6＞0}．
（Ⅰ）若A∩B={x|1＜x≤3}，求a的值；
（Ⅱ）若A∪B=B，求a的取值范围．
（Ⅰ）若A∩B={x|1＜x≤3}，求a的值；
（Ⅱ）若A∪B=B，求a的取值范围．
解：∵A={x|a≤x≤2a+3}，B={x|x2+5x﹣6＞0}=[x|x＜﹣6，或x＞1}．
（Ⅰ）依题意A∩B={x|1＜x≤3}可得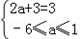
，
∴a=0．
（Ⅱ）由A∪B=B得A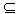
B．
①当A=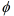
时满足题意，此时，a＞2a+3，解得a＜﹣3．
②当A≠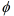
时，
，解得 a＞1．
综上，a的取值范围为：a＜﹣3 或 a＞1，即 （﹣∞，﹣3）∪（1，+∞）．
（Ⅰ）依题意A∩B={x|1＜x≤3}可得
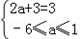，∴a=0．
（Ⅱ）由A∪B=B得A
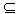B．①当A=
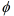时满足题意，此时，a＞2a+3，解得a＜﹣3．②当A≠
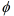时，，解得 a＞1．综上，a的取值范围为：a＜﹣3 或 a＞1，即 （﹣∞，﹣3）∪（1，+∞）．
练习册系列答案
阅读快车系列答案
相关题目