题目内容
已知x、y、z均为正数，求证：
.
证明：(证法1：综合法)因为x、y、z都是正数，所以
≥
.同理可得
＋
≥
，＋
≥
.将上述三个不等式两边分别相加，并除以2，得
(证法2：分析法)因为x、y、z均为正数，要证.只要证
≥
，只要证x2＋y2＋z2≥yz＋zx＋xy，只要证(x－y)2＋(y－z)2＋(z－x)2≥0，而(x－y)2＋(y－z)2＋(z－x)2≥0显然成立，所以原不等式成立．
练习册系列答案
相关题目
总体由编号为01,02，…，19,20的20个个体组成，利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为( )
| 7816 6572 0802 6314 0702 4369 9728 0198 |
| 3204 9234 4935 8200 3623 4869 6938 7481 |
A.08 B．07
C．02 D．01
－
.
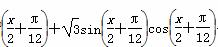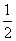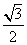，求角A，B，C；
，求证：a＞b.
的最大值．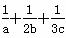
＝m，求证：a＋2b＋3c≥9.
之下的对应点的坐标为(－2，－4)，求m、k的值．
(t为参数)，若点P(m，2)在曲线C上，求m的值．