题目内容
已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C与直线l1:y=-x的一个交点的横坐标为8.
(1)求抛物线C的方程;
(2)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A、B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
解析: (1)易知直线与抛物线的交点坐标为(8,-8),∴82=2p×8,∴2p=8,∴抛物线方程为y2=8x.
(2)直线l2与l1垂直,
故可设l2:x=y+m,A(x1,y1),B(x2,y2),且直线l2与x轴的交点为M.
由 得y2-8y-8m=0,
得y2-8y-8m=0,
Δ=64+32m>0,∴m>-2.
y1+y2=8,y1y2=-8m,∴x1x2= =m2.
=m2.
由题意可知OA⊥OB,即x1x2+y1y2=m2-8m=0,∴m=8或m=0(舍),
∴l2:x=y+8,M(8,0),
故S△FAB=S△FMB+S△FMA= ·|FM|·|y1-y2|
·|FM|·|y1-y2|
=3  =24
=24 .
.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
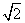 ,AC=2,若四面体ABCD体积的最大值为
,AC=2,若四面体ABCD体积的最大值为 ,则这个球的表面积为( )
,则这个球的表面积为( ) B.8π
B.8π  D.
D. 
 )来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )
)来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )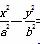 =1(a>0,b>0)的一个焦点与抛物线y2=4
=1(a>0,b>0)的一个焦点与抛物线y2=4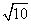 x的焦点重合,且双曲线的离心率等于
x的焦点重合,且双曲线的离心率等于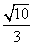 ,则该双曲线的方程为( )
,则该双曲线的方程为( )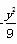 =1 B.x2-y2=15
=1 B.x2-y2=15 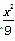 -y2=1 D.
-y2=1 D.  与
与 的大小.
的大小. .
. 有特征向量
有特征向量 ,相应的特征值为λ1,λ2.
,相应的特征值为λ1,λ2.