题目内容
8.已知函数f(x)=$\frac{1}{m}-\frac{1}{x-1}$(1)求证函数f(x)是(1,+∞)增函数;
(2)若函数f(x)在[a,b]上的值域是[2a,2b](1<a<b),求实数m的取值范围;
(3)若任意x∈[$\frac{3}{2}$,4],不等式f(x)>x恒成立,求实数m的取值范围.
(4)若存在x∈[$\frac{3}{2}$,4],使不等式f(x)>x成立,求实数m的取值范围.
分析 (1)求出函数的导数,判断导数的符号,即可得证;
(2)运用单调性,可得f(a)=2a,f(b)=2b,可得a,b为方程2x2-mx+1=0的两个不等的正根,运用韦达定理和判别式大于0,即可得到所求范围;
(3)任意x∈[$\frac{3}{2}$,4],不等式f(x)>x恒成立,即为$\frac{1}{m}$≥x+$\frac{1}{x-1}$的最大值,由单调性可得最大值;
(4)存在x∈[$\frac{3}{2}$,4],使不等式f(x)>x成立,即为即为$\frac{1}{m}$≥x+$\frac{1}{x-1}$的最小值,运用单调性即可得到所求范围.
解答 证明:(1)∵f(x)=$\frac{1}{m}-\frac{1}{x-1}$(x>1),
∴f′(x)=$\frac{1}{(x-1)^{2}}$>0在(1,+∞)上恒成立,
即f(x)在(1,+∞)为增函数;
解:(2)由f(x)在(1,+∞)为增函数,可得
f(a)=2a,f(b)=2b,
即有$\frac{1}{m}-\frac{1}{a-1}$=2a,$\frac{1}{m}-\frac{1}{b-1}$=2b,
即a,b为方程$\frac{1}{m}-\frac{1}{x-1}=2x$,即方程2mx2-(2m+1)x+(m+1)=0的两个不等的大于1的根,
则△=(2m+1)2-8m(m+1)>0,$\frac{2m+1}{4m}$>1,2m-(2m+1)+(m+1)>0
解得:0<m<$\frac{1}{2}$;
(3)任意x∈[$\frac{3}{2}$,4],不等式f(x)>x恒成立,
即为$\frac{1}{m}$≥x+$\frac{1}{x-1}$的最大值,由x+$\frac{1}{x-1}$的导数为1+$\frac{1}{(x-1)^{2}}$>0,
可得[$\frac{3}{2}$,4]为增区间,即有最大值为4+$\frac{1}{3}$=$\frac{13}{3}$,
则有0<m≤$\frac{3}{13}$;
(4)存在x∈[$\frac{3}{2}$,4],使不等式f(x)>x成立,
即为$\frac{1}{m}$≥x+$\frac{1}{x-1}$的最大小值,由x+$\frac{1}{x-1}$的导数为1+$\frac{1}{(x-1)^{2}}$>0,
可得[$\frac{3}{2}$,4]为增区间,即有最小值为2+$\frac{3}{2}$=$\frac{7}{2}$,
则有0<m≤$\frac{2}{7}$.
点评 本题考查函数的单调性的运用,考查函数的值域的求法,注意运用单调性解决,考查不等式恒成立和成立问题的解法,属于中档题.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案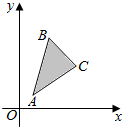 给出平面区域如图所示,其中A(1,1),B(2,5),C(4,3)若使目标函数z=ax-y仅在点C处取得最大值,则a的取值范围是$({\frac{2}{3},+∞})$.
给出平面区域如图所示,其中A(1,1),B(2,5),C(4,3)若使目标函数z=ax-y仅在点C处取得最大值,则a的取值范围是$({\frac{2}{3},+∞})$.