题目内容
定长为3的线段AB的端点A、B在抛物线y2=x上移动,求AB的中点到y轴的距离的最小值,并求出此时AB中点的坐标.
解:如图,设F是y2=x的焦点,A、B两点到准线的垂线分别是AC、BD.
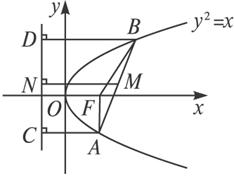
又M到准线的垂线为MN,C、D和N是垂足,则|MN|=![]() (|AC|+|BD|)=
(|AC|+|BD|)=![]() (|AF|+|BF|)≥
(|AF|+|BF|)≥![]() |AB|=
|AB|=![]() .
.
设M点的横坐标为x,纵坐标为y,|MN|=x+![]() ,则x≥
,则x≥![]() -
-![]() =
=![]() ,而等式成立的条件是AB过点F.
,而等式成立的条件是AB过点F.
当x=![]() 时,y1y2=-p2=-
时,y1y2=-p2=-![]() ,
,
故(y1+y2)2=y12+y22+2y1y2=2x-![]() =2,
=2,
∴y1+y2=±![]() ,y=±
,y=±![]() .∴M(
.∴M(![]() ,?±
,?±![]() ),此时M到y轴的距离的最小值为
),此时M到y轴的距离的最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =x上移动,AB的中点为M,求点M到y轴的最短距离,并求出此时点M的坐标.
=x上移动,AB的中点为M,求点M到y轴的最短距离,并求出此时点M的坐标.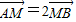 .
.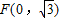 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.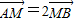 .
.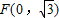 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.