题目内容
定长为3的线段AB的两端点在抛物线y2=x上移动,记线段AB的中点为M,求点M到y轴的最短距离,并求此时点M的坐标.分析:先用A、B点的坐标表示点M,则点M到y轴的距离即为其横坐标建立距离模型,再利用基本不等式法求得最值,由取得等号的条件求得M点的坐标.
解答:解:设A(x1,y1),B(x2,y2),AB长度为3,
那么x1=y12,x2=y22,(1)
32=(x2-x1)2+(y2-y1)2=(y22-y12)2+(y2-y1)2=(y2-y1)2[(y2+y1)2+1](2)
线段AB的中点M(x,y)到y轴的距离为x=
=
(
+
)=
[(y1-y2)2+((y1+y2)2+1)-1]≥
[2
-1]
由(2)得x≥
(2×3-1)=
,并且当(y1-y2)2=(y1+y2)2+1=3(3)
时x取得最小值x0=
下证x能达到最小值,根据题意不妨设y1>y2,由(3)得
由此解得y1,y2,由(1)解得x1,x2,所以x可取得最小值
.
相应的M点纵坐标y0=
=±
∴M点坐标为(
,
)或(
,-
)
那么x1=y12,x2=y22,(1)
32=(x2-x1)2+(y2-y1)2=(y22-y12)2+(y2-y1)2=(y2-y1)2[(y2+y1)2+1](2)
线段AB的中点M(x,y)到y轴的距离为x=
| x1+x2 |
| 2 |
| 1 |
| 2 |
| y | 2 1 |
| y | 2 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| (y1-y2)2((y1+y2)2+1) |
由(2)得x≥
| 1 |
| 4 |
| 5 |
| 4 |
时x取得最小值x0=
| 5 |
| 4 |
下证x能达到最小值,根据题意不妨设y1>y2,由(3)得
|
由此解得y1,y2,由(1)解得x1,x2,所以x可取得最小值
| 5 |
| 4 |
相应的M点纵坐标y0=
| y1+y2 |
| 2 |
| ||
| 2 |
∴M点坐标为(
| 5 |
| 4 |
| ||
| 2 |
| 5 |
| 4 |
| ||
| 2 |
点评:本题主要考查建模和解模的能力.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 =x上移动,AB的中点为M,求点M到y轴的最短距离,并求出此时点M的坐标.
=x上移动,AB的中点为M,求点M到y轴的最短距离,并求出此时点M的坐标.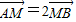 .
.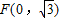 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.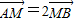 .
.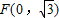 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.