题目内容
定长为3的线段AB两端点A、B分别在x轴,y轴上滑动,M在线段AB上,且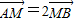 .
.(1)求点M的轨迹C的方程;
(2)设过
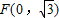 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
【答案】分析:(1)设A(x1,0),B(0,y1),M(x,y),则 ,由此能求出点M的轨迹C的方程.
,由此能求出点M的轨迹C的方程.
(2)设满足条件的点D(0,m),设l的方程为: ,代入椭圆方程,得
,代入椭圆方程,得 ,设
,设 ,
, .由以DA、DB为邻边的平行四边形为菱形,知
.由以DA、DB为邻边的平行四边形为菱形,知 ,由此能导出存在满足条件的点D.
,由此能导出存在满足条件的点D.
解答:解:(1)设A(x1,0),B(0,y1),M(x,y)
则 ,|AB|=3=
,|AB|=3= =1
=1
(2)存在满足条件的D点.设满足条件的点D(0,m),
则 ,设l的方程为:y=kx+
,设l的方程为:y=kx+ ,(k≠0),代入椭圆方程,
,(k≠0),代入椭圆方程,
得(k2+4)x2+2 kx-1=0,设A(x1,y1),B(x2,y2),则x1+x2=-
kx-1=0,设A(x1,y1),B(x2,y2),则x1+x2=- ,
,
∴y1+y2=k(x1+x2)+2 .∵以DA、DB为邻边的平行四边形为菱形,
.∵以DA、DB为邻边的平行四边形为菱形,
∴ ,
, =
= ,
, 的方向向量为(1,k),
的方向向量为(1,k), =0,
=0,
∴- -2mk=0即m=
-2mk=0即m= ∵k2>0,∴m=
∵k2>0,∴m= ,∴0<m<
,∴0<m< ,∴存在满足条件的点D.
,∴存在满足条件的点D.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
 ,由此能求出点M的轨迹C的方程.
,由此能求出点M的轨迹C的方程.(2)设满足条件的点D(0,m),设l的方程为:
 ,代入椭圆方程,得
,代入椭圆方程,得 ,设
,设 ,
, .由以DA、DB为邻边的平行四边形为菱形,知
.由以DA、DB为邻边的平行四边形为菱形,知 ,由此能导出存在满足条件的点D.
,由此能导出存在满足条件的点D.解答:解:(1)设A(x1,0),B(0,y1),M(x,y)
则
 ,|AB|=3=
,|AB|=3= =1
=1(2)存在满足条件的D点.设满足条件的点D(0,m),
则
 ,设l的方程为:y=kx+
,设l的方程为:y=kx+ ,(k≠0),代入椭圆方程,
,(k≠0),代入椭圆方程,得(k2+4)x2+2
 kx-1=0,设A(x1,y1),B(x2,y2),则x1+x2=-
kx-1=0,设A(x1,y1),B(x2,y2),则x1+x2=- ,
,∴y1+y2=k(x1+x2)+2
 .∵以DA、DB为邻边的平行四边形为菱形,
.∵以DA、DB为邻边的平行四边形为菱形,∴
 ,
, =
= ,
, 的方向向量为(1,k),
的方向向量为(1,k), =0,
=0,∴-
 -2mk=0即m=
-2mk=0即m= ∵k2>0,∴m=
∵k2>0,∴m= ,∴0<m<
,∴0<m< ,∴存在满足条件的点D.
,∴存在满足条件的点D.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
 轴,
轴, 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且
 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段 上
上 轴,
轴, 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且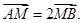
 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段 上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。
上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。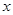 轴,
轴,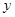 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且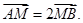
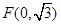 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线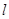 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段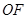 上
上