题目内容
19. 已知函数y=2sin($\frac{x}{2}$+$\frac{π}{4}$).
已知函数y=2sin($\frac{x}{2}$+$\frac{π}{4}$).(1)求函数取得最小值时自变量x的值;
(2)当-$\frac{5}{6}$π≤x≤$\frac{5}{6}$π时.求函数的值域;
(3)求函数的单调递增区间;
(4)用“五点法”作出函数在长度为一个周期的闭区间上的简图;
(5)请逐一写出由函数y=sinx的图象得到y=2sin($\frac{x}{2}$+$\frac{π}{4}$)的图象的变换过程.
分析 (1)由$\frac{x}{2}$+$\frac{π}{4}$=2kπ-$\frac{π}{2}$,k∈Z,可解得函数取得最小值时自变量x的值.
(2)由-$\frac{5}{6}$π≤x≤$\frac{5}{6}$π.可求$\frac{x}{2}$+$\frac{π}{4}$∈[-$\frac{π}{6}$,$\frac{2π}{3}$],利用正弦函数的图象和性质即可求函数的值域;
(3)由2kπ-$\frac{π}{2}$≤$\frac{x}{2}$+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z,可解得函数的单调递增区间.
(4)列表,描点,连线,用五点法即可作函数f(x)在一个周期上的简图.
(5)把y=sinx的图象向左平移$\frac{π}{4}$个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),再把各点的纵坐标变为原来的3倍(横坐标不变),即得函数y=2sin($\frac{x}{2}$+$\frac{π}{4}$)的图象.
解答 解:(1)由$\frac{x}{2}$+$\frac{π}{4}$=2kπ-$\frac{π}{2}$,k∈Z,可解得:x∈{x|x=4kπ-$\frac{3π}{2}$,k∈Z}时,函数取得最小值为-2.
(2)∵-$\frac{5}{6}$π≤x≤$\frac{5}{6}$π.
∴$\frac{x}{2}$+$\frac{π}{4}$∈[-$\frac{π}{6}$,$\frac{2π}{3}$],
∴sin($\frac{x}{2}$+$\frac{π}{4}$)∈[-$\frac{1}{2}$,1].可得:y=2sin($\frac{x}{2}$+$\frac{π}{4}$)函数的值域为:[-1,2].
(3)由2kπ-$\frac{π}{2}$≤$\frac{x}{2}$+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z,可解得函数的单调递增区间为:[4kπ-$\frac{3π}{2}$,4kπ+$\frac{π}{2}$],k∈Z.
(4)列表:
| $\frac{x}{2}$+$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{2}$ | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ |
| y | 0 | 2 | 0 | -2 | 0 |
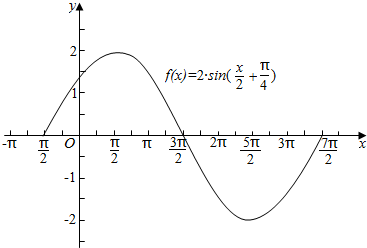
(5)把y=sinx的图象向左平移$\frac{π}{4}$个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),
再把各点的纵坐标变为原来的2倍(横坐标不变),即得函数y=2sin($\frac{x}{2}$+$\frac{π}{4}$)的图象.
点评 本题主要考查了函数y=Asin(ωx+φ)的图象变换,正弦函数的图象和性质,五点法作函数y=Asin(ωx+φ)的图象,属于基本知识的考查.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案| A. | a<-8 | B. | a>-8 | C. | -8<a<5 | D. | a<-8或a>5 |