题目内容
19.(1)解方程:log2(4x+4)=x+log2(2x+1-3)(2)解不等式:log2(log3(log4x))<0.
分析 (1)由$x=lo{g}_{2}{2}^{x}$,log2(4x+4)=x+log2(2x+1-3),可得4x+4=2x(2x+1-3),化简解出即可得出.
(2)由log2(log3(log4x))<0,可得x>0,log3(log4x)<1,利用对数的运算性质及其单调性进一步化简即可得出.
解答 解:(1)∵$x=lo{g}_{2}{2}^{x}$,log2(4x+4)=x+log2(2x+1-3),∴4x+4=2x(2x+1-3),∴(2x)2-3•2x-4=0,2x>0,
解得2x=4,解得x=2,经过检验满足条件.
∴原方程的解为:x=2.
(2)∵log2(log3(log4x))<0,
∴x>0,log3(log4x)<1,
∴x>0,log4x<3,
∴x>0,x<43,
因此0<x<64.
点评 本题考查了对数的运算性质及其单调性、方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
9.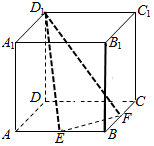 如图,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,过点D1、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为V1、V2(V1<V2),则V1:V2=( )
如图,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,过点D1、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为V1、V2(V1<V2),则V1:V2=( )
 如图,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,过点D1、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为V1、V2(V1<V2),则V1:V2=( )
如图,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,过点D1、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为V1、V2(V1<V2),则V1:V2=( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{25}{47}$ | D. | $\frac{7}{9}$ |
10.已知x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y-2≤0\end{array}\right.$,则z=$\frac{y+1}{x+1}$的范围是( )
| A. | $[\frac{1}{3},2]$ | B. | $[-\frac{1}{2},\frac{1}{2}]$ | C. | $[\frac{1}{2},\frac{3}{2}]$ | D. | $[\frac{3}{2},\frac{5}{2}]$ |
4.$tanϕ=-\sqrt{3}$,ϕ为第四象限角,则cosϕ=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
11.某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
| 每件产品A | 每件产品B | ||
| 研制成本、搭载 费用之和(万元) | 20 | 30 | 计划最大资金额 300万元 |
| 产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
| 预计收益(万元) | 80 | 60 |
9. 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准,为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:),样本统计结果如图表:
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准,为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:),样本统计结果如图表:
(I)分别求出n,a,b的值;
(II)若从样本中月均用水量在[5,6](单位:)的5位居民中任选2人作进一步的调查研究,求月均用水量最多的居民被选中的概率(5位居民的月均用水量均不相等).
 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准,为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:),样本统计结果如图表:
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准,为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:),样本统计结果如图表:| 分组 | 频数 | 频率 |
| [0,1) | a | |
| [1,2) | 0.19 | |
| [2,3) | 50 | b |
| [3,4) | 0.23 | |
| [4,5) | 0.18 | |
| [5,6) | 5 |
(II)若从样本中月均用水量在[5,6](单位:)的5位居民中任选2人作进一步的调查研究,求月均用水量最多的居民被选中的概率(5位居民的月均用水量均不相等).