题目内容
【题目】如图,等腰直角三角形ABC所在的平面与半圆弧AB所在的平面垂直,AC⊥AB,P是弧AB上一点,且∠PAB=30°.
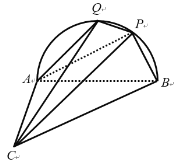
(1)证明:平面BCP⊥平面ACP;
(2)若Q是弧AP上异于AP的一个动点,当三棱锥C-APQ体积最大时,求二面角A-PQ-C的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)根据等腰直角三角形ABC所在的平面与半圆弧AB所在的平面垂直,AC⊥AB,得到![]() 平面APB,从而
平面APB,从而![]() ,又
,又![]() ,由线面垂直的判定定理得到
,由线面垂直的判定定理得到![]() 平面ACP,再由面面垂直的判定定理证明.
平面ACP,再由面面垂直的判定定理证明.
(2)由(1)知![]() 平面APB,若三棱锥C-APQ体积最大,则三角形APQ面积最大,此时
平面APB,若三棱锥C-APQ体积最大,则三角形APQ面积最大,此时![]() 为
为![]() 的中点,过点A作
的中点,过点A作![]() ,连接
,连接![]() ,得到
,得到![]() 平面ACE,从而
平面ACE,从而![]() 为二面角A-PQ-C的平面角,根据∠PAB=30°,设AC=2,求得AE,CE即可.
为二面角A-PQ-C的平面角,根据∠PAB=30°,设AC=2,求得AE,CE即可.
(1)因为等腰直角三角形ABC所在的平面与半圆弧AB所在的平面垂直,AC⊥AB,
所以![]() 平面APB,又PB
平面APB,又PB![]() 平面APB,
平面APB,
所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面ACP,又
平面ACP,又![]() 平面BCP,
平面BCP,
所以平面BCP⊥平面ACP;
(2)由(1)知![]() 平面APB,
平面APB,
所以AC为三棱锥C-APQ的高,设![]()
若三棱锥C-APQ体积最大,则三角形APQ面积最大
当![]() 为
为![]() 的中点时,三角形APQ面积最大,
的中点时,三角形APQ面积最大,
如图所示:
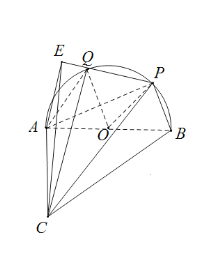
过点A作![]() ,连接
,连接![]() ,
,
所以![]() 平面ACE,
平面ACE,
所以![]() 为二面角A-PQ-C的平面角,
为二面角A-PQ-C的平面角,
因为∠PAB=30°.
所以![]() ,
,
所以![]() ,
,![]()
所以![]() ,
,
所以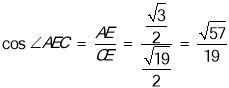 .
.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目