题目内容
[2012·江苏高考]已知函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为________.
9
通过值域求a,b的关系是关键.
由题意知f(x)=x2+ax+b=(x+ )2+b-
)2+b- .
.
∵f(x)的值域为[0,+∞),∴b- =0,即b=
=0,即b= .
.
∴f(x)=(x+ )2.
)2.
又∵f(x)<c,∴(x+ )2<c,
)2<c,
即- -
- <x<-
<x<- +
+ .
.
∴
②-①,得2 =6,∴c=9.
=6,∴c=9.
由题意知f(x)=x2+ax+b=(x+
 )2+b-
)2+b- .
.∵f(x)的值域为[0,+∞),∴b-
 =0,即b=
=0,即b= .
.∴f(x)=(x+
 )2.
)2.又∵f(x)<c,∴(x+
 )2<c,
)2<c,即-
 -
- <x<-
<x<- +
+ .
.∴

②-①,得2
 =6,∴c=9.
=6,∴c=9.
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π. ,求f(θ)的值;
,求f(θ)的值; 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.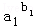
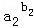 …
…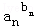 ≤1;
≤1; ≤
≤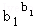
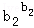 …
…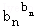 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2.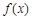 的定义域为
的定义域为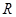 ,若存在常数
,若存在常数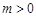 ,对任意
,对任意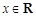 ,有
,有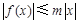 ,则称
,则称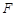 函数.给出下列函数:
函数.给出下列函数: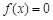 ; ②
; ②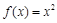 ; ③
; ③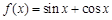 ; ④
; ④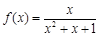 ;
;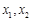 均有
均有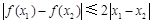 .其中是
.其中是 ),B=[
),B=[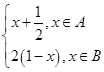 ,若x0∈A,且f[f(x0)]∈A,则x0的取值范围是( )
,若x0∈A,且f[f(x0)]∈A,则x0的取值范围是( ) ]
] ]
]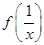 =-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数:
=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数: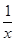 ;②y=x+
;②y=x+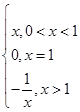 ,其中满足“倒负”变换的函数是________(填序号).
,其中满足“倒负”变换的函数是________(填序号). ,则使f[f(x)]=2成立的实数x的集合为________.
,则使f[f(x)]=2成立的实数x的集合为________.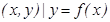 },若对于任意
},若对于任意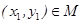 ,存在
,存在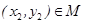 ,使得
,使得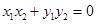 成立,则称集合M是“垂直对点集”.给出下列四个集合:
成立,则称集合M是“垂直对点集”.给出下列四个集合: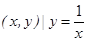 };
};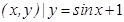 };
};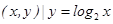 };
};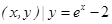 }.
}.  与函数
与函数 的图像分别交于点
的图像分别交于点 ,则当
,则当 达到最小时
达到最小时 的值为( )
的值为( )

