题目内容
已知定义域为 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:
(1) 对任意的 ,总有
,总有 ;(2)
;(2) ;(3) 若
;(3) 若 ,
, ,且
,且 ,则有
,则有 成立,则称
成立,则称 为“友谊函数”,请解答下列各题:
为“友谊函数”,请解答下列各题:
(1)若已知 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;
(2)函数 在区间
在区间 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知 为“友谊函数”,假定存在
为“友谊函数”,假定存在 ,使得
,使得 且
且 , 求证:
, 求证: .
.
 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:(1) 对任意的
 ,总有
,总有 ;(2)
;(2) ;(3) 若
;(3) 若 ,
, ,且
,且 ,则有
,则有 成立,则称
成立,则称 为“友谊函数”,请解答下列各题:
为“友谊函数”,请解答下列各题:(1)若已知
 为“友谊函数”,求
为“友谊函数”,求 的值;
的值; (2)函数
 在区间
在区间 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.(3)已知
 为“友谊函数”,假定存在
为“友谊函数”,假定存在 ,使得
,使得 且
且 , 求证:
, 求证: .
.(1) (2)是友谊函数(3)见解析.
(2)是友谊函数(3)见解析.
 (2)是友谊函数(3)见解析.
(2)是友谊函数(3)见解析.试题分析:(1)利用赋值法由
 得
得 ,再由
,再由 得
得 ,所以
,所以 (2)分别验证(1)由指数函数的性质
(2)分别验证(1)由指数函数的性质 在区间
在区间 上的最小值为0,(2)直接带入验证易得
上的最小值为0,(2)直接带入验证易得 (3)利用做差法直接比较
(3)利用做差法直接比较
 (3) 先利用单调性的定义证明抽象函数的单调性,然后再证明
(3) 先利用单调性的定义证明抽象函数的单调性,然后再证明
取
 得
得 , 又由
, 又由 ,
,得

(2)显然
 在
在 上满足(1)
上满足(1)  ;(2)
;(2) .(3)若
.(3)若 ,
, ,且
,且 ,则有
,则有

故
 满足条件(1)、(2)、(3),所以
满足条件(1)、(2)、(3),所以 为友谊函数.
为友谊函数.(3)由 (3)知任给
 其中
其中 ,且有
,且有 ,不妨设
,不妨设

所以:
 .
.下面证明
 :(i)若
:(i)若 ,则有
,则有 或
或
若
 ,则
,则 ,这与
,这与 矛盾;
矛盾; (2)若
 ,则
,则 ,这与
,这与 矛盾;
矛盾; 综上所述:


练习册系列答案
相关题目
 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π. ,求f(θ)的值;
,求f(θ)的值; 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.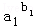
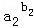 …
…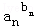 ≤1;
≤1; ≤
≤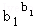
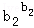 …
…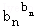 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2.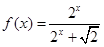 .
.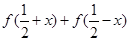 的值;
的值;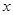 的不等式:
的不等式: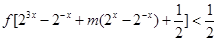 在区间
在区间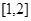 上有解,求实数
上有解,求实数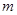 的取值范围.
的取值范围.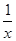 +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.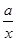 ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围. 个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中
个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中 ,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.
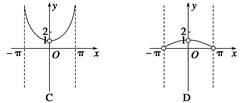
,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.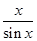 ,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )
,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )
 取得最小值.
取得最小值.