题目内容
已知实数x,y满足约束条件y≤x,x+2y≥-2,则s=(x+1)2+(y-1)2的最小值是 .
考点:点到直线的距离公式
专题:计算题,直线与圆
分析:画出不等式组
表示的平面区域,s=(x+1)2+(y-1)2的几何意义是区域内的点与点(-1,1)的距离的平方.由图象过(-1,1)作直线y=x的垂线,求出点(-1,1)到直线y=x的距离,即可得到最小值.
|
解答:
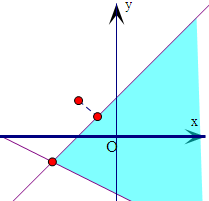 解:画出不等式组
解:画出不等式组
表示的平面区域,
s=(x+1)2+(y-1)2的几何意义是
区域内的点与点(-1,1)的距离的平方.
由图象过(-1,1)作直线y=x的垂线,则点(-1,1)到直线y=x的距离即为最小,且为
=
,
则s=(x+1)2+(y-1)2的最小值为:2.
故答案为:2
 解:画出不等式组
解:画出不等式组
|
s=(x+1)2+(y-1)2的几何意义是
区域内的点与点(-1,1)的距离的平方.
由图象过(-1,1)作直线y=x的垂线,则点(-1,1)到直线y=x的距离即为最小,且为
| |1-(-1)| | ||
|
| 2 |
则s=(x+1)2+(y-1)2的最小值为:2.
故答案为:2
点评:本题考查不等式组表示的平面区域,考查点到直线的距离和两点的距离公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
| 1 |
| 2 |
| A、2+2i | B、2-2i |
| C、i | D、-i |
抛物线y2=2px三点的纵坐标的平方成等差数列,则这三点的横坐标( )
| A、成等差数列 |
| B、成等比数列 |
| C、即成等差数列又成等比数列 |
| D、即不成等差数列又不成等比数列 |
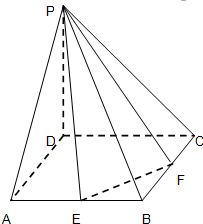 已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=2,E,F分别是AB和BC的中点.
已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=2,E,F分别是AB和BC的中点.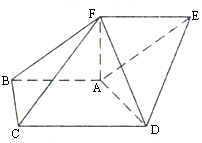 在五面体ABCDEF中,AB∥DC,∠BAD=
在五面体ABCDEF中,AB∥DC,∠BAD=