题目内容
证明:空间不共点且两两相交的四条直线在同一平面内.
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:四条直线两两相交包括:四条直线中有三条相交于一点与四条直线中任何三条都不共点两种情况.
无论哪种情况先由两直线相交确定一个平面,再通过直线上两点在一个平面内则该直线在这个平面内,即可证明.
无论哪种情况先由两直线相交确定一个平面,再通过直线上两点在一个平面内则该直线在这个平面内,即可证明.
解答:
 证明:设四条直线分别为a,b,c,d
证明:设四条直线分别为a,b,c,d
(1)若当四条直线中有三条相交于一点,
不妨设a,b,c相交于一点A,
但A∈d,如图1.
∴直线d和A确定一个平面α.
又设直线d与a,b,c分别相交于E,F,G,
则A,E,F,G∈α.
∵A,E∈α,且A,E∈a∴a?α.
同理可证b?α,c?α.
∴a,b,c,d在同一平面α内.
(2)当四条直线中任何三条都不共点时,如图2.
∵这四条直线两两相交,则设相交直线a,b确定一个平面α.
设直线c与a,b分别交于点H,K,则H,K∈α.
又H,K∈c,∴c?α.
同理可证d?α.
∴a,b,c,d四条直线在同一平面α内.
 证明:设四条直线分别为a,b,c,d
证明:设四条直线分别为a,b,c,d(1)若当四条直线中有三条相交于一点,
不妨设a,b,c相交于一点A,
但A∈d,如图1.
∴直线d和A确定一个平面α.
又设直线d与a,b,c分别相交于E,F,G,
则A,E,F,G∈α.
∵A,E∈α,且A,E∈a∴a?α.
同理可证b?α,c?α.
∴a,b,c,d在同一平面α内.
(2)当四条直线中任何三条都不共点时,如图2.
∵这四条直线两两相交,则设相交直线a,b确定一个平面α.
设直线c与a,b分别交于点H,K,则H,K∈α.
又H,K∈c,∴c?α.
同理可证d?α.
∴a,b,c,d四条直线在同一平面α内.
点评:本题主要考查平面的确定方法、线在面内的判定方法及分类讨论思想.

练习册系列答案
相关题目
函数f(x)=2sin(2x-
)的图象上的点的横坐标变成原来的4倍(纵坐标不变)再图象上的点向左平移
个单位,向下平移1个单位以后得到的函数的一个对称轴方程为( )
| π |
| 6 |
| π |
| 3 |
A、x=
| ||
B、x=
| ||
| C、x=π | ||
| D、x=2π |
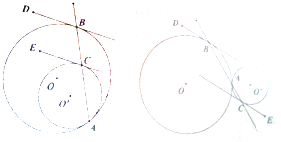 已知:如图,⊙O和⊙O′相切于点A,直线AB和⊙O的另一个交点为B,和⊙O′的另一个交点为C,BD,CE分别切⊙O′,⊙O于点B,C.求证:BD∥CE.研究:两圆外切时结论还成立吗?
已知:如图,⊙O和⊙O′相切于点A,直线AB和⊙O的另一个交点为B,和⊙O′的另一个交点为C,BD,CE分别切⊙O′,⊙O于点B,C.求证:BD∥CE.研究:两圆外切时结论还成立吗?