题目内容
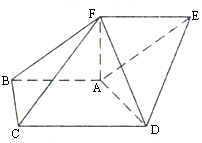 在五面体ABCDEF中,AB∥DC,∠BAD=
在五面体ABCDEF中,AB∥DC,∠BAD=| π |
| 2 |
| 7 |
(Ⅰ)求两异面直线BF与DE所成角的余弦值;
(Ⅱ)FC与平面FAD的所成角的正弦值.
考点:直线与平面所成的角,异面直线及其所成的角
专题:空间角
分析:(Ⅰ)以A为原点,AB为x轴,AD为y轴,AF为z轴,建立空间直角坐标系,利用向量法能求出两异面直线BF与DE所成角的余弦值.
(Ⅱ)求出
=(2,2,-1),平面FAD的法向量
=(1,0,0),利用向量法能求出FC与平面FAD的所成角的正弦值.
(Ⅱ)求出
| FC |
| n |
解答:
解:(Ⅰ)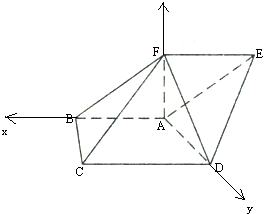 ∵AB∥DC,∠BAD=
∵AB∥DC,∠BAD=
,∴CD⊥AD;
又∵FA⊥平面ABCD,
由三垂线定理知CD⊥FD,
∴CD⊥面FAD,
在Rt△ABC中,FD=
=
=
,
由FA⊥平面ABCD,得FA⊥AD,
在Rt△FAD中,FA=
=
=1,
由FA⊥平面ABCD,得FA⊥AD,
又由∠BAD=
,得AD⊥AB,
∴AD⊥平面ABFE,∴DA⊥AE,
在Rt△AED中,AE=
=
=
,
∵四边形ABFE为平行四边形,
∴BF=AE=
,AB=EF=
=
,
由题意,以A为原点,AB为x轴,AD为y轴,
AF为z轴,建立空间直角坐标系,
则B(
,0,0),F(0,0,1),D(0,2,0),E(-
,0,1),
∴
=(-
,0,1),
=(-
,-2,1),
∴cos<
,
>=
=
,
∴两异面直线BF与DE所成角的余弦值为
.
(Ⅱ)由已知得C(2,2,0),
∴
=(2,2,-1),
平面FAD的法向量
=(1,0,0),
设FC与平面FAD的所成角为θ,
则sinθ=|cos<
,
>|=
.
∴FC与平面FAD的所成角的正弦值为
.
 ∵AB∥DC,∠BAD=
∵AB∥DC,∠BAD=| π |
| 2 |
又∵FA⊥平面ABCD,
由三垂线定理知CD⊥FD,
∴CD⊥面FAD,
在Rt△ABC中,FD=
| FC2-CD2 |
| 9-4 |
| 5 |
由FA⊥平面ABCD,得FA⊥AD,
在Rt△FAD中,FA=
| FD2-AD2 |
| 5-4 |
由FA⊥平面ABCD,得FA⊥AD,
又由∠BAD=
| π |
| 2 |
∴AD⊥平面ABFE,∴DA⊥AE,
在Rt△AED中,AE=
| ED2-AD2 |
| 7-4 |
| 3 |
∵四边形ABFE为平行四边形,
∴BF=AE=
| 3 |
| 3-1 |
| 2 |
由题意,以A为原点,AB为x轴,AD为y轴,
AF为z轴,建立空间直角坐标系,
则B(
| 2 |
| 2 |
∴
| BF |
| 2 |
| DE |
| 2 |
∴cos<
| BF |
| DE |
| 2+0+1 | ||||
|
| ||
| 7 |
∴两异面直线BF与DE所成角的余弦值为
| ||
| 7 |
(Ⅱ)由已知得C(2,2,0),
∴
| FC |
平面FAD的法向量
| n |
设FC与平面FAD的所成角为θ,
则sinθ=|cos<
| FC |
| n |
| 2 |
| 3 |
∴FC与平面FAD的所成角的正弦值为
| 2 |
| 3 |
点评:本题考查两异面直线所成角的余弦值的求法,考查直线与平面所成角的正弦值的求法,是中档题,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
函数f(x)=2sin(2x-
)的图象上的点的横坐标变成原来的4倍(纵坐标不变)再图象上的点向左平移
个单位,向下平移1个单位以后得到的函数的一个对称轴方程为( )
| π |
| 6 |
| π |
| 3 |
A、x=
| ||
B、x=
| ||
| C、x=π | ||
| D、x=2π |
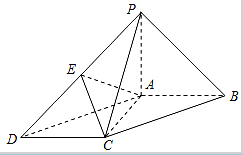 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点. 某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185),得到的频率分布直方图如图所示.
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185),得到的频率分布直方图如图所示.