题目内容
已知 f（x）=
，不等式f（x+a）＞f（2a-x）在[a，a+1]上恒成立，则a的取值范围是 ．
|
考点：函数恒成立问题,分段函数的应用
专题：不等式的解法及应用
分析：作出分段函数的图象，由图象得到函数f（x）的单调性，然后把不等式f（x+a）＞f（2a-x）在[a，a+1]上恒成立转化为不等式a＞2（a+1）求解．
解答：
解：作出分段函数f（x）=
的图象如图，
要使不等式f（x+a）＞f（2a-x）在[a，a+1]上恒成立，
则x+a＜2a-x在x∈[a，a+1]上恒成立，
即a＞2x在x∈[a，a+1]上恒成立，
∴a＞2（a+1），解得：a＜-2．
故答案为：（-∞，-2）．
|
要使不等式f（x+a）＞f（2a-x）在[a，a+1]上恒成立，
则x+a＜2a-x在x∈[a，a+1]上恒成立，
即a＞2x在x∈[a，a+1]上恒成立，
∴a＞2（a+1），解得：a＜-2．
故答案为：（-∞，-2）．
点评：本题考查了恒成立问题，考查了分段函数的应用，解答此题的关键是把恒成立问题转化为含a的不等式，是中档题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
A、B是锐角三角形的两个内角，则直线xsinA-ycosB=0的倾斜角（ ）
| A、大于135° |
| B、大于90°且小于135° |
| C、大于45°且小于90° |
| D、小于45° |
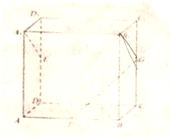如图，长方体ABCD-A1B1C1D1中，AA1=AB=2，AD=1，E，F，G分别是DD1，AB，CC1的中点，则异面直线A1E与GF所成角为