题目内容
设函数f(x)=
(Ⅰ)当a=-5时,求函数f(x)的定义域;
(Ⅱ)若函数f(x)的定义域为R,试求a的取值范围.
| |x+1|+|x-2|+a |
(Ⅰ)当a=-5时,求函数f(x)的定义域;
(Ⅱ)若函数f(x)的定义域为R,试求a的取值范围.
考点:函数恒成立问题,函数的定义域及其求法
专题:计算题,函数的性质及应用
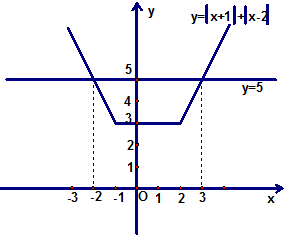
分析:(Ⅰ)易知|x+1|+|x-2|-5≥0,在同一坐标系中作出函数y=|x+1|+|x-2|和y=5 的图象,由图象可求;
(Ⅱ)由题意可知|x+1|+|x-2|≥-a恒成立,由图象求出|x+1|+|x-2|的最小值即可;
(Ⅱ)由题意可知|x+1|+|x-2|≥-a恒成立,由图象求出|x+1|+|x-2|的最小值即可;
解答:
 解:(Ⅰ)由题设知:|x+1|+|x-2|-5≥0,
解:(Ⅰ)由题设知:|x+1|+|x-2|-5≥0,
如图,在同一坐标系中作出函数y=|x+1|+|x-2|和y=5 的图象(如图所示)
得定义域为(-∞,-2]∪[3,+∞).
(Ⅱ)由题设知,当x∈R 时,恒有|x+1|+|x-2|+a≥-a,即|x+1|+|x-2|≥-a,
又由(Ⅰ)知|x+1|+|x-2|≥3,
当且仅当 (x+1)(x-2)≤0,即-1≤x≤2取等号,
∴-a≤3⇒a≥-3.
 解:(Ⅰ)由题设知:|x+1|+|x-2|-5≥0,
解:(Ⅰ)由题设知:|x+1|+|x-2|-5≥0,如图,在同一坐标系中作出函数y=|x+1|+|x-2|和y=5 的图象(如图所示)
得定义域为(-∞,-2]∪[3,+∞).
(Ⅱ)由题设知,当x∈R 时,恒有|x+1|+|x-2|+a≥-a,即|x+1|+|x-2|≥-a,
又由(Ⅰ)知|x+1|+|x-2|≥3,
当且仅当 (x+1)(x-2)≤0,即-1≤x≤2取等号,
∴-a≤3⇒a≥-3.
点评:该题卡函数的定义域及其求法,考查函数恒成立问题,考查数形结合思想.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知i是虚数单位,复数
的模为( )
| -5+i |
| 2-3i |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
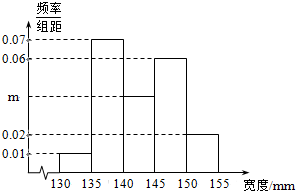 1895年,在伦敦有100块男性头盖骨被挖掘出土,经考证,头盖骨的主人死于1665-1666年之间的大瘟疫.人类学家分别测量了这些头盖骨的宽度,得到的频率分布直方图如图所示.
1895年,在伦敦有100块男性头盖骨被挖掘出土,经考证,头盖骨的主人死于1665-1666年之间的大瘟疫.人类学家分别测量了这些头盖骨的宽度,得到的频率分布直方图如图所示.