题目内容
15.甲乙对弈,每局甲赢概率为$\frac{1}{3}$,乙赢概率为$\frac{2}{3}$,三局两胜制,则甲获胜概率为( )| A. | $\frac{7}{27}$ | B. | $\frac{2}{9}$ | C. | $\frac{2}{27}$ | D. | $\frac{1}{3}$ |
分析 甲获胜是指甲连胜两局或甲在前两局中一胜一平,第三局甲胜,由此能求出结果.
解答 解:甲乙对弈,每局甲赢概率为$\frac{1}{3}$,乙赢概率为$\frac{2}{3}$,三局两胜制,
则甲获胜概率为:
p=$(\frac{1}{3})^{2}+{C}_{2}^{1}(\frac{1}{3})(\frac{2}{3})(\frac{1}{3})$=$\frac{7}{27}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意在n次独立试验中事件A恰好发生k次的概率计算公式的合理运用.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
6.某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站10km处建仓库,则土地费用和运输费用分别为2万元和8万元,那么要使两项费用之和最小,仓库应建在离车站( )
| A. | 5 km处 | B. | 4 km处 | C. | 3 km处 | D. | 2 km处 |
3.已知i为虚数单位,复数z满足$z+zi=|\sqrt{3}-i|$,则复数z对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
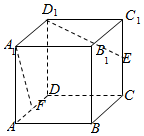 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是CC1,AD的中点,那么异面直线D1E和A1F所成角的余弦值等于$\frac{2}{5}$.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是CC1,AD的中点,那么异面直线D1E和A1F所成角的余弦值等于$\frac{2}{5}$.