题目内容
在 中,角
中,角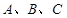 对边分别是
对边分别是 ,满足
,满足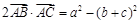 .
.
(1)求角 的大小;
的大小;
(2)求 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角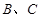 的大小.
的大小.
(1)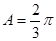 ;(2)
;(2)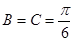 .
.
解析试题分析:(1)由向量的数量积计算出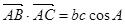 ,再结合余弦定理
,再结合余弦定理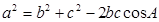 化简
化简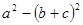 ,两式相结合得出
,两式相结合得出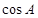 的值,求角
的值,求角 的大小;
的大小;
(2)由(1)的值,得出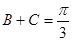 的值,将原式表示成关于
的值,将原式表示成关于 或
或 的式子,通过
的式子,通过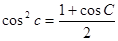 进行化简,结合化一公式将函数化简成
进行化简,结合化一公式将函数化简成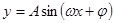 的形式,结合角
的形式,结合角 的大小,
的大小,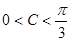 ,求出函数的最值.同时求出取得最大值时的角
,求出函数的最值.同时求出取得最大值时的角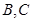 的大小.
的大小.
试题解析:(1)由已知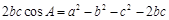 ,
,
由余弦定理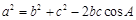 得
得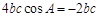 ,∴
,∴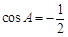 , 2分
, 2分
∵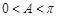 ,∴
,∴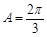 . 4分
. 4分
(2)∵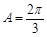 ,∴
,∴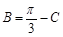 ,
,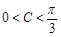 .
.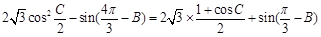
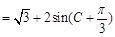 . 8分
. 8分
∵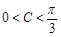 ,∴
,∴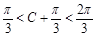 ,∴当
,∴当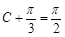 ,
,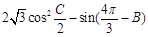 取最大值
取最大值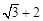 ,
,
此时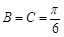 . 12分
. 12分
考点:1.三角函数的化简;2.三角函数的性质.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
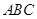 中,角
中,角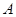 ,
,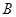 ,
, 的对边分别是
的对边分别是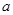 ,
,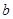 ,
,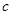 ,且
,且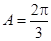 ,
,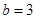 ,△
,△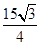 .
.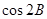 的值.
的值.
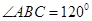 ,
,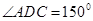 ,
,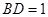 (千米),
(千米),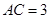 (千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.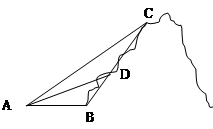
 中,
中, 是边
是边 的中点,且
的中点,且 ,
, .
.
 的值;
的值; 的值.
的值. 中,角
中,角 的对边分别为
的对边分别为 .已知
.已知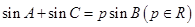 ,且
,且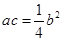 .
. 时,求
时,求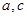 的值;
的值;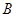 为锐角,求
为锐角,求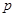 的取值范围.
的取值范围. 中,角
中,角 、
、 、
、 所对的边长分别为
所对的边长分别为 、
、 、
、 ,
,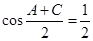 .
.  ,
, ,求
,求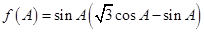 ,求
,求 的取值范围.
的取值范围. 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 ,
, .
. 的大小;
的大小; ,
, ,求
,求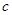 边的长和△
边的长和△ b.
b.