题目内容
在△ 中,角
中,角 、
、 、
、 所对的边长分别为
所对的边长分别为 、
、 、
、 ,
,
且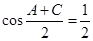 .
.
(1)若 ,
, ,求
,求 的值;
的值;
(2)若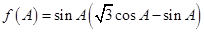 ,求
,求 的取值范围.
的取值范围.
(1) 或
或 ;(2)
;(2)
 .
.
解析试题分析:(1)已知两边,要求第三边,最好能求出已知两边的夹角,然后用余弦定理可求得,而由已知条件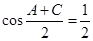 可得
可得 ,从而可知
,从而可知 ,即
,即 ,问题得解;(2)这是三角函数的一般性问题,解决它的一般方法是把函数化为
,问题得解;(2)这是三角函数的一般性问题,解决它的一般方法是把函数化为 的形式,然后利用正弦函数的知识解决问题,
的形式,然后利用正弦函数的知识解决问题, ,首先用二倍角公式,降幂公式把二次式化为一次式
,首先用二倍角公式,降幂公式把二次式化为一次式

 ,再利用两角和的正弦公式把两个三角函数化为一个三角函数,
,再利用两角和的正弦公式把两个三角函数化为一个三角函数, ,接下来我们只要把
,接下来我们只要把 作为一个整体,求出它的范围,就可借助于正弦函数求出
作为一个整体,求出它的范围,就可借助于正弦函数求出 的取值范围了.
的取值范围了.
试题解析:(1)在△ 中,
中, .
.
所以
 .
. ,所以
,所以 . 3分
. 3分
由余弦定理 ,得
,得 .
.
解得 或
或 . 6分
. 6分
(2)

 . 9分
. 9分
由(1)得 ,所以
,所以 ,
, ,
,
则 . ∴
. ∴ .∴
.∴ .
.
∴ 的取值范围是
的取值范围是 . 12分
. 12分
考点:(1)余弦定理;(2)二倍角公式与降幂公式,三角函数的取值范围

练习册系列答案
相关题目
 ,
, .
. 的值.
的值. 到
到 ,方位角(从正北方向顺时针转到
,方位角(从正北方向顺时针转到 方向所成的角)是
方向所成的角)是 ,距离是3km;从
,距离是3km;从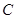 ,方位角是110°,距离是3km;从
,方位角是110°,距离是3km;从 ,方位角是140°,距离是(
,方位角是140°,距离是( )km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
)km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号). 中,角
中,角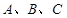 对边分别是
对边分别是 ,满足
,满足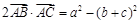 .
. 的大小;
的大小; 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角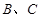 的大小.
的大小. 中,内角
中,内角 对边的长分别是
对边的长分别是 ,且
,且 .
. ,求
,求 ;
; ,求
,求 .
. 的最小正周期;
的最小正周期;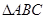 中,若
中,若 的值.
的值. .
. 的最大值及最小正周期;
的最大值及最小正周期; ,
, ,求
,求 的值.
的值.
 ,△ABC的面积为
,△ABC的面积为 ,求
,求 .
. km的C、D两点,并且测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.
km的C、D两点,并且测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.